
Федеральное агентство по образованию
Санкт-Петербургский государственный горный институт им. Г.В. Плеханова
(технический университет)

(наименование учебной дисциплины согласно учебному плану)
Выполнил: студент гр.ЭР-06-2 / Поддубный Д.А./
(подпись) (Ф.И.О.)
Оценка:
(должность) (подпись) (Ф.И.О.)
Санкт-Петербург
2008
Дано: тело Ω, расположенное в первом октанте и ограниченное
координатными плоскостями и поверхностью Σ, заданной уравнением ![]() и векторное поле
и векторное поле ![]()
Задание:
Решение:
1) Нахождение потока:
1-ый способ.
Поверхность Σ пересекает положительные координатные полуоси в точках ![]() ,
, ![]() ,
,
![]() .
.
Параметризуем поверхность Σ, полагая, что:
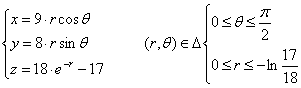
Так как поверхность взаимно однозначно проектируется на любую координатную плоскость то поток поля через эту поверхность можно определить вычислением следующего интеграла:
![]() ,
,
Где:
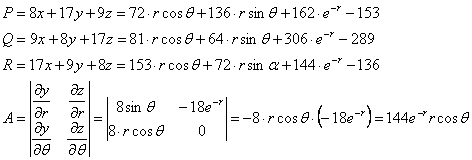
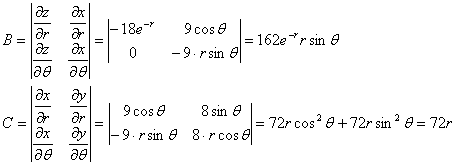
Таким образом:

Определим поток через плоскую область М1М2О:

Потоки через область М2М3О и М3М1О:

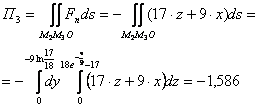
Таким образом, поток через поверхность тела равен:
![]()
2-ой способ. По формуле Гаусса – Остроградского:
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.