Вариант №9
|
x |
-5,705 |
-4,841 |
-3,976 |
-3,112 |
-2,247 |
-1,383 |
-0,518 |
0,346 |
1,211 |
|
y |
0,035 |
0,052 |
0,095 |
0,130 |
0,220 |
0,509 |
0,677 |
0,992 |
1,745 |
|
lny |
-3,352 |
-2,956 |
-2,353 |
-2,040 |
-1,514 |
-0,675 |
-0,390 |
-0,008 |
0,557 |
Подобрать такую
формулу (из ![]() ,
, ![]() ,
, ![]() ), чтобы вычисленные по ней значения
при
), чтобы вычисленные по ней значения
при ![]() возможно мало отличались от значений
возможно мало отличались от значений
![]() табличной функции.
табличной функции.
Если
выбранную функциональную зависимость обозначить ![]() ,
где
,
где ![]() - параметры функции, то согласно
методу наименьших квадратов наилучшими коэффициентами
- параметры функции, то согласно
методу наименьших квадратов наилучшими коэффициентами ![]() будут
те, для которых сумма
будут
те, для которых сумма ![]() будет
минимальной.
будет
минимальной.
Используя
необходимые условия экстремума функции нескольких переменных, получим
нормальную систему Гаусса для определения коэффициентов ![]() :
:
![]() .
.
В случае линейной
зависимости ![]() , где
, где ![]() -
неизвестные параметры, нормальная система примет вид:
-
неизвестные параметры, нормальная система примет вид:
 ;
;
 ;
;
|
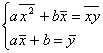 ,
,
где 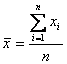 ,
, 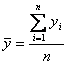 ,
, 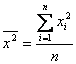 ,
,
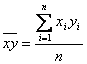 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.