Критерий устойчивости Вышнеградского в системе MatLAB

 

Министерство образования Российской Федерации

Государственное образовательное учреждение

высшего профессионального образования

“Комсомольский-на-Амуре государственный

технический университет”

Кафедра “Судовые энергетические установки”

Лабораторная работа №2

Критерий устойчивости Вышнеградского

в системе MatLAB

Студент группы 0ТЭ                                                    А.В. Балута

Преподаватель                                                              А.А. Малыхин

2004

 

Содержание

Содержание……………………………………………………………………………..2

1.  Общие условия устойчивости линейных САР……………………………………3

2.  Понятие критериев устойчивости и их виды……………………………………...3

3.  Критерий устойчивости Вышнеградского………………………………………...4

4.  Программа и графики…….………………………………………………………...5

 

1. Общие условия устойчивости линейных САР

Устойчивость линейных систем определяется устойчивостью их свободного движения. Устойчивой называется такая система, которая будучи выведенной из состояния равновесия, через определенное время возвращается к прежнему значению регулируемого параметра.

Математически это означает, что решив уравнение динамики свободного движения

( [W(p) + 1])y = 0 (*), мы должны убедиться, что:

При   t → ∞    y → 0

Уравнение (*) является однородным. Общее решение однородного д.у. с постоянными коэффициентами представляет функцию вида:

y = C1e  +  C2e   +  …  +  Cne  ,

Ci – постоянная интегрирования;

ri – корни характеристического уравнения анализируемого д.у..

Среди корней характеристического уравнения в общем случае могут быть:

а) чисто вещественные вида                      r = R

б) комплексные сопряженные                    r = ρ ± jω

в) чисто мнимые вида                                 r = jω

Анализ поведения составляющих общего решения д.у. свободного движения во времени показывает, что для устойчивости линейных динамических систем необходимым и достаточным является условие, чтобы корни характеристического уравнения исходного д.у. свободного движения анализируемой динамической системы были бы либо вещественными отрицательными, либо комплексными с отрицательной вещественной частью. При чисто мнимых корнях система находится на границе устойчивости.

2. Понятие критериев устойчивости и их виды

Из необходимого и достаточного условия устойчивости линейных систем следует, что для решения вопроса об устойчивости требуется знать не численные значения корней, а только их знаки.

Искусственные математические методы анализа алгебраических характеристических уравнений динамических систем, позволяющие определить знаки корней без решения характеристических уравнений, называются критериями устойчивости динамических систем.

Они подразделяются на 3 вида:

- алгебраические критерии устойчивости (Гурвица, Раусса);

- параметрические критерии устойчивости (Вышнеградского, D-разбиения);

- частотные критерии устойчивости.

3. Критерий устойчивости Вышнеградского

Параметрические критерии устойчивости, в отличие от алгебраических, не только отвечают на вопрос устойчива система или нет, но и показывает насколько близка или далека граница от устойчивости, можно ли неустойчивую систему сделать устойчивой или повысить запас устойчивости и показывает примерный вид переходного процесса в системе.

Критерий Вышнеградского относится только к динамическим системам, описываемых д.у. 3-его порядка. Т.е., когда д.у. свободного движения замкнутой системы описывается уравнением вида:

х уравнений динамических систем, позволяющие опре д.у. ешение одноролногднородным. вижения, мы должны убедиться, что:нное время возвращается к прежнему значению регулируемого п

 

(*)

Т1, Т2, Т3 – постоянные времени системы;

Вышнеградский, введя так называемое безразмерное время      τ = t/T1 , преобразовал (*) к виду:

X,Y – параметры Вышнеградского;

Характеристическое уравнение преобразованного д.у.:

r + Xr + Yr +1 = 0

Решая характеристическое уравнение для всех реально возможных значений параметров X,Y, он построил диаграммуВышнеградского.

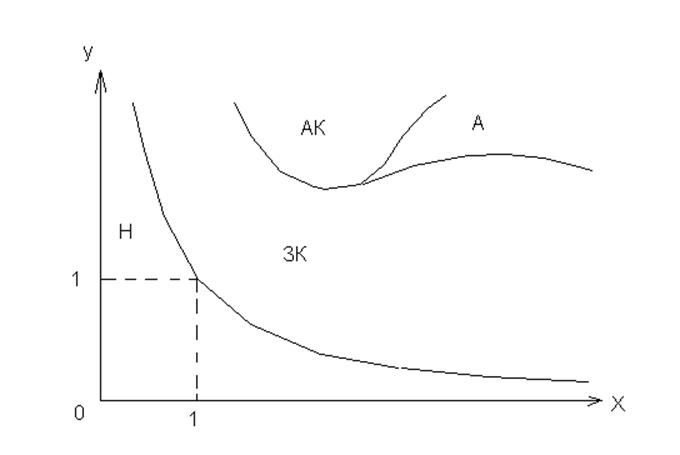
Критерий устойчивости Вышнеградского имеет вид:     XY> 1

 

4. Программа и графики

Рассмотрим 2 случая.

1)  В области Н.

h1=tf(5,[1 0,7 0,5 1])

step(h1)

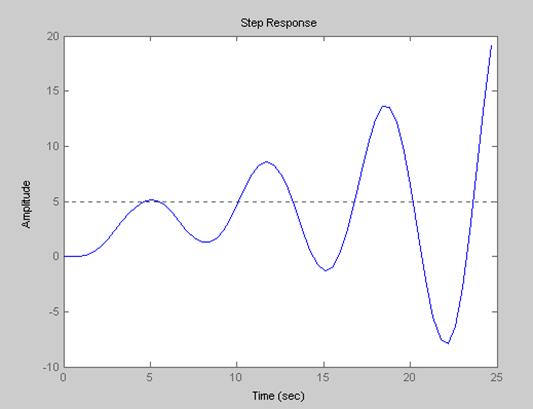
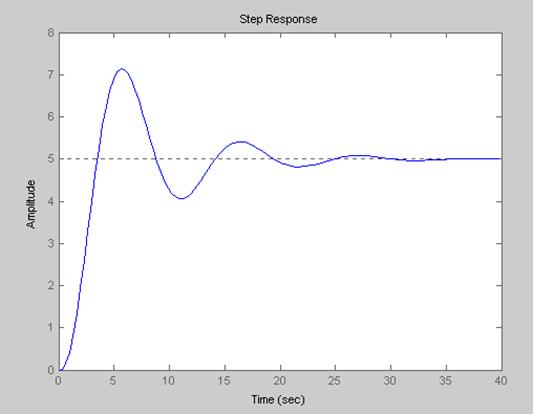
2)  В области ЗК.

h2=tf(5,[1 3 1.2 1])

step(h2)