Лабораторний практикум
по дисциплiнi
“Схемотехніка ЕОМ”
(з використанням пакету
Electronic Workbench)
Лабораторна робота № DE-2
Вивчення особливостей роботи і
використання мультиплексорів
2. Основні теоретичні положення
 Мультиплексором називається цифровий комбінаційний
пристрій призна-чений для прийому інформації з декількох паралельних ліній і
передачі її в одну вихідну в вигляді впорядкованої послідовності.Вибір
відповідної вхідної лінії та її гальвонічне з’єднання з вихідною забезпечується
відповідним адресним кодом. При наявності n адресних входів
комбінаційною схемою мультиплексора забезпечується комбінація 2n
ліній передачі інформації.
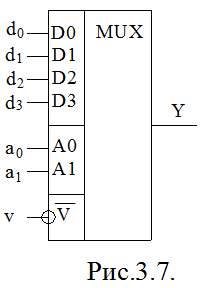
На рис 3.7 приведене умовне зображення мультиплексора, призначеного для
комутації одного з 4-х інформаційних входів D0 – D3 на
вихід Y з допомогою двох адресних сигналів А0 та А1
. Вхід V являється допоміжним входом і називається
дозво-ляючим. При сигналі на вході v=0 мультиплексор виконує свої функції , а при v
= 1 інформація з D0 – D3 на вихід Y не
передається. Робота мультиплексора описується логічною функцією:
Мультиплексором називається цифровий комбінаційний
пристрій призна-чений для прийому інформації з декількох паралельних ліній і
передачі її в одну вихідну в вигляді впорядкованої послідовності.Вибір
відповідної вхідної лінії та її гальвонічне з’єднання з вихідною забезпечується
відповідним адресним кодом. При наявності n адресних входів
комбінаційною схемою мультиплексора забезпечується комбінація 2n
ліній передачі інформації.
На рис 3.7 приведене умовне зображення мультиплексора, призначеного для
комутації одного з 4-х інформаційних входів D0 – D3 на
вихід Y з допомогою двох адресних сигналів А0 та А1
. Вхід V являється допоміжним входом і називається
дозво-ляючим. При сигналі на вході v=0 мультиплексор виконує свої функції , а при v
= 1 інформація з D0 – D3 на вихід Y не
передається. Робота мультиплексора описується логічною функцією:
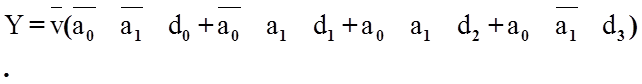 |
 З формули (3.10) витікає, що зміна кодів на входах А0,А1
, яка відбувається в відповідності з частотою генератора адресних сигналів а0,а1
, приводить до частового розподілення інформаційних сигналів d0 – d3 на
виході Y.(часто сигнали d0 – d3називають
“данними”).
З формули (3.10) витікає, що зміна кодів на входах А0,А1
, яка відбувається в відповідності з частотою генератора адресних сигналів а0,а1
, приводить до частового розподілення інформаційних сигналів d0 – d3 на
виході Y.(часто сигнали d0 – d3називають
“данними”).
Приведена схема може виконувати і дещо іншу функцію- цілеспрямовано вибирати дані по окремій, або декількох окремих адресах. В такому випадку подібні пристрої називаються селекторами ( від select- вибирати).
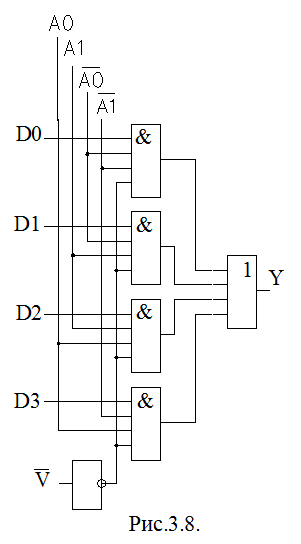
Дозволяючий вхід V розширює можли-вості приcтрою. Він дозволяє синхронізувати роботу мультиплексора з іншими схемами, а також використовується для нарощування роз-рядності адресних сипгналів. Логічна схема мультиплексора, реалізована в базисі І-НІ-АБО в відповідності до формули (3.10), приведена на рис. 3.8.
Кількість інформаційних входів мульти-плексора відображається в його назві. Напри-клад, розглянута схема відповідає назві “ з 4-х в 1”, або просто “4:1”. В залежності від кількості інформаційних входів, вони бувають “з 8 в 1”, “з 16 в 1” і т.д.
Так як мультиплексор являється комбіна-ційною схемою, то на його базі можуть виконуватись різні логічні функції. Як прикладом їх реалізації скорис-таємось формулою (3.10). Допустимо, що необхідно реалізувати логічну функцію:
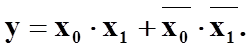
(3.11)
 Порівнюючи формули (3.11) і (3.10) бачимо, що
присвоївши адресним сигналам а0,а1 значення х0,х1
і забезпечивши d1 =
d3 =
0, d0 =
d2 =
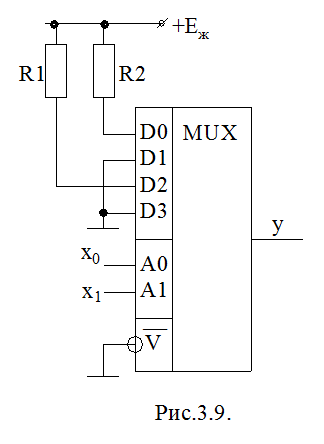
1, v =0, одержимо схему, (рис.3.9), яка реалізує
функцію (3.11).
Порівнюючи формули (3.11) і (3.10) бачимо, що
присвоївши адресним сигналам а0,а1 значення х0,х1
і забезпечивши d1 =
d3 =
0, d0 =
d2 =
1, v =0, одержимо схему, (рис.3.9), яка реалізує
функцію (3.11).
Нескладні перетворення логічних функцій дають можливість реалізову-вати на мультиплексорах функції з кількістю змінних, що перевершує кількість адресних входів. Виконується слідуюча послідовність перетворень:
· в мінімізованій діз’юнктивній нор-мальній формі функції виділяються змінні, які мають найвищий ранг, тобто повторюються в найбільшій кількості діз’юнкцій. Наприклад, вибирається m змінних;
· ![]()
виконується перетворення функції так,
щоб забезпечити присутність виділених змінних в усіх діз’юнкціях . Для цього
кожна діз’юнкція домножається на
· проводиться перегрупування логічної функції завдяки тому, що виділені змінні виносяться за дужки в відповідних групах діз’юнкцій.
В результаті виконаних перетворень одержується формула вихідної функ-ції, яка реалізується на мультиплексорі “ з M=2m в 1”, якщо на його адресні входи подати виділені змінні, а на інформаційних входах забезпечується вико-наня тих логічних виразів, які залишились в дужках. Якщо вирази в дужках являються функціями декількох змінни, тоїх реалізація може бути забезпечена або з допомогою іншого мультиплексора, або на основі типових логічних елементів.
Приклад. Функцію
Реалізувати з використанням мультиплексора “з 4-х в 1”.
Так як в використовуємому мультиплексорі два адресні входи, то виби-раємо дві змінні з найбільшими рангами. Ранги змінних приведені в табл. 3.1.
Табл. 3.1. Вибираємо дві змінні х2 та х3 .
|
х0 |
х1 |
х2 |
х3 |
х4 |
|
3 |
2 |
3 |
4 |
2 |
Виконуємо перетворення функції:
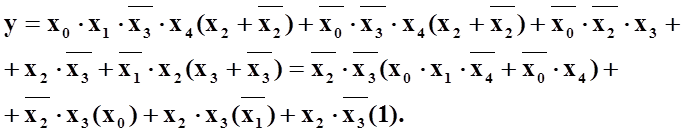 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.