Министерство образования науки
Национальный аэрокосмический университет
им. Н.Е. Жуковского
кафедра 304
Лабораторная работа №14
по предмету
«Численные методы»
Выполнила студентка
Группы 325
Абкеримова Рушена
Проверила: преподаватель кафедры 304
Яровая Ольга Владимировна
Харьков 2014
Лабораторная работа №1
«Методы решения ОДЕ и СОДЕ»
Вариант №1
Цель работы: с помощью методов Эйлера, уточненного метода Эйлера, формул Милна, Рунге-Кутта, Аддамса научиться вычислять корни диференциального уравнения и систем обыкновенных диференциальных уравнений.
Mathcad:
Для ОДУ:
|
Ч и с л е н н о е р е ш е н и е о б ы к н о в е н н ы х д и ф ф е р е н ц и а л ь н ы х у р а в н е н и й . |
|
И с х о д н ы е д а н н ы е |
|
|
|
|
|
|
|
Ш а г : |
|
|
|
; |
|
|
|
|
|
|
|
|
|
1. Р е ш е н и е О Д У с п о м о щ ь ю с т а н д а р т н о г о б л о к а |
|
|
|
|
|
|
|
|
|
|
|
|
|
2. П р о г р а м м н ы й б л о к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С п л а й н о в а я и н т е р п о л я ц и я : |
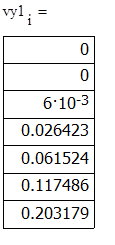
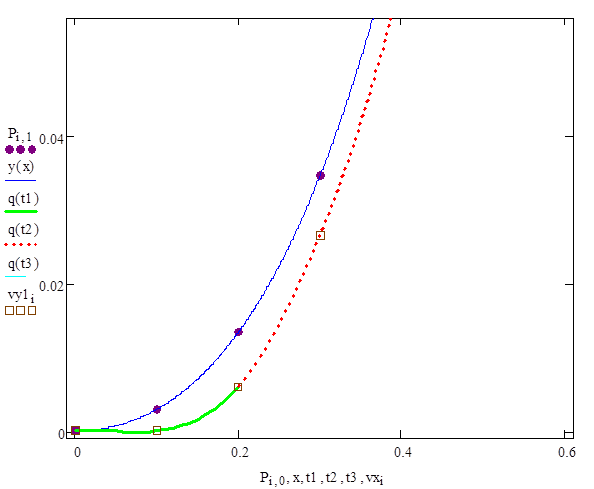
Для решения СОДУ:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И с х о д н ы е д а н н ы е . |
|
|
|
|
|
Н а ч а л ь н о е у с л о в и е : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Matlab:
Функция записи оду:
function res = f(x,y)
res = ((x+y)^2)+0.5*(x+y);
return
function res = ODE(x0,y0,n,h);
vx = zeros(n,1);
for i = 1:n
vx(i) = x0+(i-1)*h;
end;
vy = zeros(n,1);
vy(1) = y0;
for i = 1:2
vy(i+1)=vy(i) + h*f(vx(i),vy(i));
end;
for i = 3:4
vy(i+1) = vy(i) + h/2*(f(vx(i),vy(i))+f(vx(i+1),vy(i)+h*f(vx(i),vy(i))));
end;
K = zeros(4,1);
for i=5:6
K(1) = h*f(vx(i),vy(i));
K(2) = h*f(vx(i)+h/2,vy(i)+K(1)/2);
K(3) = h*f(vx(i)+h/2,vy(i)+K(2)/2);
K(4) = h*f(vx(i)+h,vy(i)+K(3));
vy(i+1) = vy(i)+1/6*(K(1)+2*(K(2)+K(3))+K(4));
end;
xx = vx(1):0.01:vx(n);
pp = interp1(vx,vy,'cubic','pp');
yy = ppval(pp,xx);
plot(vx,vy,'ko'),hold on, plot(xx,yy,'-'),grid on,hold on;
res = vy;
return
>> y=ODE(0,0,7,0.1)
y =
0
0
0.0060
0.0264
0.0615
0.1175
0.2032
>> [t,y]=ode45(@f,[0 0.5],0)
t =
0
0.0125
0.0250
0.0375
0.0500
0.0625
0.0750
0.0875
0.1000
0.1125
0.1250
0.1375
0.1500
0.1625
0.1750
0.1875
0.2000
0.2125
0.2250
0.2375
0.2500
0.2625
0.2750
0.2875
0.3000
0.3125
0.3250
0.3375
0.3500
0.3625
0.3750
0.3875
0.4000
0.4125
0.4250
0.4375
0.4500
0.4625
0.4750
0.4875
0.5000
y =
0
0.0000
0.0002
0.0004
0.0007
0.0011
0.0016
0.0022
0.0029
0.0037
0.0047
0.0058
0.0070
0.0084
0.0099
0.0115
0.0133
0.0153
0.0175
0.0198
0.0224
0.0251
0.0280
0.0312
0.0346
0.0382
0.0420
0.0461
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.