Министерство образования Российской Федерации
Санкт-Петербургский государственный горный институт им. Г.В. Плеханова
(технический университет)
Расчетно-графическое задание №1:
Вариант 12.
студент группы АПМ-03 _____________ Никифоров М.Н.
(подпись) (Ф.И.О)
Санкт-Петербург
2004
Исходные данные:
|
x |
0,006 |
0,014 |
0,032 |
0,072 |
0,165 |
0,376 |
0,857 |
1,954 |
4,454 |
10,152 |
|
y |
0,155 |
0,192 |
0,331 |
0,399 |
0,542 |
0,663 |
1,109 |
1,065 |
1,917 |
2,646 |
Решение:
Построив точечную диаграмму по исходным данным, можно сделать вывод, что зависимость между x и y не является линейной, т.к. по графику функций, построенному по этим точкам, не просматривается прямая.
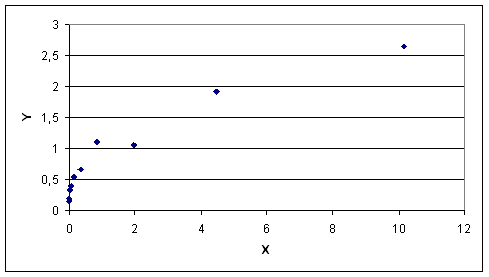
Выясним, имеет ли место экспоненциальная зависимость y(x), для этого построим точечную диаграмму в осях x и lny, получим:
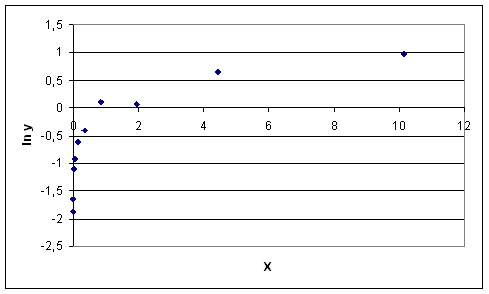
Следовательно, экспоненциальной зависимости между x и y нет.
Построим точечную диаграмму в осях ln x и ln y:
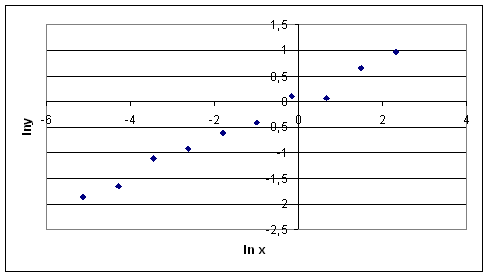
Построив
данный график, можно сказать, что имеет место степенная зависимость, т.е. ![]() , т.к. соединив все точки на графике,
получится приблизительно прямая.
, т.к. соединив все точки на графике,
получится приблизительно прямая.
Логарифмируя
выражение ![]() , получим:
, получим: ![]() .
.
Полагая,
что ![]() , получим зависимость:
, получим зависимость: ![]() .
.
Используя
систему: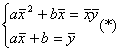 ,
где
,
где 
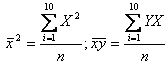 ,
найдем значения параметров a и B.
Для этого найдем все значения
,
найдем значения параметров a и B.
Для этого найдем все значения ![]() и
и ![]() и занесем полученные значения в
таблицу:
и занесем полученные значения в
таблицу:
|
lnx |
-5,11599581 |
-4,268697949 |
-3,442019376 |
-2,63108916 |
-1,801809805 |
-0,978166136 |
|
lny |
-1,864330162 |
-1,650259907 |
-1,105636904 |
-0,918793862 |
-0,612489278 |
-0,410980289 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.