Практическая работа № 2.
Изучение вероятностных методов описания транспортных систем
Теоретические сведения.
Дискретной случайной величиной называется действительная функция ![]() , определенная на дискретном
пространстве элементарных событий:
, определенная на дискретном
пространстве элементарных событий:![]() , где m=
, где m=![]() . В результате некоторого испытания
(наблюдения, опыта) наступает какое-то одно элементарное событие
. В результате некоторого испытания
(наблюдения, опыта) наступает какое-то одно элементарное событие ![]() из
из ![]() .
Функция
.
Функция ![]() преобразует его в вещественное число
преобразует его в вещественное число ![]() , которое и воспринимается как случайная
величина Х.
, которое и воспринимается как случайная
величина Х.
На практике чаще удобно работать не с исходным
пространством элементарных событий ![]() , а с множеством
возможных значений
, а с множеством
возможных значений ![]() случайной величины Х и
вероятностями
случайной величины Х и
вероятностями ![]() , которые принимаются случайной
величиной Х:
, которые принимаются случайной
величиной Х:
![]() ,
, ![]() . (1)
. (1)
Распределением вероятностей дискретной случайной величины Х называется
система равенств (1), для которой ![]() удовлетворяют условиям
неотрицательности и нормировки.
удовлетворяют условиям
неотрицательности и нормировки.
Распределение вероятностей (1) для конечнозначной
случайной величины (то есть, если ![]() ) может быть задано в
виде таблицы (табл.1) или графически (в виде полигона частот – рис.1).
) может быть задано в
виде таблицы (табл.1) или графически (в виде полигона частот – рис.1).
Пусть дискретная случайная величина Х значение ![]() приняла
приняла ![]() раз,
значение
раз,
значение ![]() –
– ![]() раза и
т.д. Тогда частотой события Х =
раза и
т.д. Тогда частотой события Х =![]() называется
отношение
называется
отношение
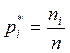 , (2)
, (2)
где
![]() (общее число наблюдений, или объем
выборки).
(общее число наблюдений, или объем
выборки).
Группировкой данных называется разбиение интервала, содержащего n наблюдений дискретной случайной величины X на некоторое число интервалов m и подсчет числа наблюдений, попавших в каждый из образовавшихся интервалов.
Если обозначить длины интервалов ![]() ,
, ![]() ,…,
,…,![]() , а середины интервалов группирования
, а середины интервалов группирования ![]() ,
, ![]() ,…,
,…,![]() , то число наблюдений
, то число наблюдений ![]() , попавших в
, попавших в
j-й интервал есть число наблюдений x, удовлетворяющих
неравенству
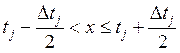 , (3)
, (3)
или
![]() ,
,
где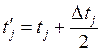 – правый конец j-го интервала
группирования,
– правый конец j-го интервала
группирования, 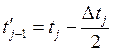 – его левый конец, j=1,2,...,m.
– его левый конец, j=1,2,...,m.
Частотой наблюдений ![]() в j-м интервале группирования
называется отношение числа наблюдений, попавших в j-й интервал, к общему числу наблюдений n:
в j-м интервале группирования
называется отношение числа наблюдений, попавших в j-й интервал, к общему числу наблюдений n:
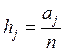 . (4)
. (4)
Относительной частотой называется величина
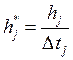 . (5)
. (5)
Накопленной частотой ![]() , соответствующей j-му интервалу, называется
сумма наблюдений в первом, втором,…, j-м интервалах. Иными словами, это частота наблюдений,
не выходящих за пределы границы j-го интервала группирования
, соответствующей j-му интервалу, называется
сумма наблюдений в первом, втором,…, j-м интервалах. Иными словами, это частота наблюдений,
не выходящих за пределы границы j-го интервала группирования 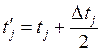 :
:
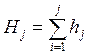 .
(6)
.
(6)
Гистограммой распределения дискретной случайной величины, или гистограммой относительных частот называется графической изображение (рис.2) функции:
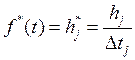 при
при 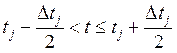 . (7)
. (7)
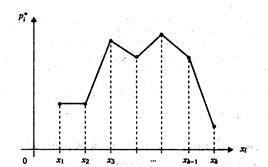
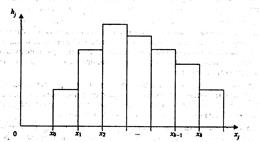
Рис.1 Рис.2
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.