Вопрос №9
Способ построения проекции перпендикуляра, опущенного из точки М на треугольник общего положения АВС
Пример 2. Задана точка D и проекции треугольника АВС. Требуется определить расстояние от точки D до плоскости треугольника АВС.
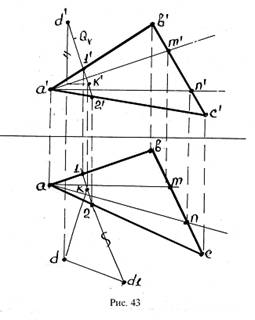
Решение: Из точки D опускается перпендикуляр на плоскость треугольника АВС. Для построения проекций перпендикуляра используются горизонталь и фронталь треугольника АВС (АМ, AN, рис. 43).
Определяется точка встречи перпендикуляра с плоскостью треугольника АВС. С этой целью через фронтальную проекцию перпендикуляра проводится вспомогательная фронтально-проектирующая плоскость Q. Эта плоскость пересекает стороны треугольника АВС в точках 1, 2 (см. рис. 43).
На горизонтальной проекции определяется точка пересечения перпендикуляра с линией 1-2 (точка k, см. рис. 43).
Определяется натуральная величина отрезка DК, которая представляет расстояние от точки D до плоскости треугольника АВС.
Вопрос №10
Построение сечения поверхности плоскостью общего положения методом ребер. Привести пример.
Вопрос №31
Развертка пирамиды методом треугольников. Пояснить на примере.
Рассматривается пример построения линии пересечения пирамиды плоскостью общего положения Р (рис. 73 а).
Через ребро SC проводится горизонтально – проектирующая плоскость Q и определяется линия пересечения плоскостей P и Q – линия 1 –2.
На фронтальной проекции определяется точка пересечения линии 1¢ - 2¢ с ребром S¢C¢ - точка m¢ (см. рис 73 а).
Через ребро sb проводится проектирующая плоскость S и определяется линия пересечения плоскостей S и Р – линия 3 – 4. Находится точка пересечения линии 3¢ - 4¢ с ребром s¢b¢ - точка n¢.
Через ребро s¢a¢ проводится фронтально – проектирующая плоскость R и строится линия пересечения плоскостей R и Р – линия 5 – 6. Определяется точка пересечения линии 5 - 6 с ребром sa – точка К.
На горизонтальной и фронтальной проекциях точки KMN соединяются прямыми. В результате построения получают проекции сечения пирамиды плоскостью.
Развертка пирамиды выполняется способом прямоугольников. Вначале определяются натуральные размеры ребер пирамиды способом плоско – параллельного перемещения: точка S перемещается параллельно оси Х в положение S1 (см. рис. 72 а). Прямая SA разворачивается вокруг точки S1 до положения, когда она станет параллельной оси Х – положение s1a1. Аналогично определяются положения ребер s1b1 и s1c1.
Определяются фронтальные проекции точек SABC - s¢1, a¢1, b¢1, c¢1. Соединив вершину s¢1 с точкой основания пирамиды, получают натуральные величины ребер s¢1 a¢1, s¢1 b¢1, s¢1 c¢1.
На полученные линии проектируются точки k¢, n¢, m¢ - k¢1, n¢1, m¢1.
Развертка пирамиды выполняется путем последовательного построения ее граней, совмещенных с плоскостью проекции:
Проводится базовая линия. На ней отмечаются точки S и А. Размер отрезка SA снимается с фронтальной проекции - s¢1 a¢1.
Строится грань SAB – из точки S радиусом R1 = s¢1 b¢1 строится дуга окружности. Из точки А радиусом r1 = sa наносится вторая дуга окружности. Пересечение двух дуг окружностей определяет положение точки В.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.