Вопрос №2 Способ определения расстояния от вершины наклонной пирамиды до ее основания
Пример 2. Заданы проекции пирамиды SABC. Требуется определить:
1) Угол a° наклона основания пирамиды к фронтальной плоскости проекций;
2) Расстояние L1 от вершины пирамиды до ее основания;
3) Построить проекции перпендикуляра, опущенного из точки S на плоскость АВС;
4) Площадь основания пирамиды;
5) Угол b° наклона ребра SC пирамиды к ее основанию;
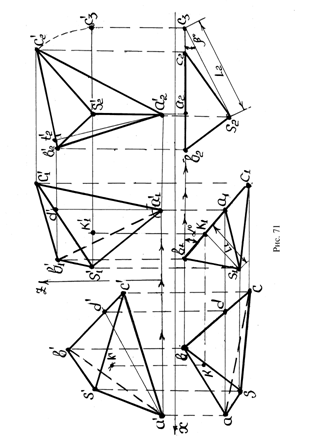
6) Длину L2 ребра SC пирамиды (рис 71).
Решение: Через точку а проводится фронталь ad.
За полюс фигуры принимается точка а¢. За направление перемещения – линия а¢1а¢, параллельная оси Х.
Полюс фигуры – точка а¢ перемещается в положение а¢1.
Фигура разворачивается вокруг полюса так, чтобы фронталь а¢d¢ стала перпендикулярной оси Х.
Строится новая фронтальная проекция фигуры - s¢1a¢1b¢1c¢1 (см. рис. 71). Построение ведется из условия, что при перемещении и повороте фигуры взаимное расположение ее точек на фронтальной проекции не изменилось.
На горизонтальной проекции размечаются траектории движений точек а,b,c – линии, параллельные оси Х. На эти линии проецируются соответствующие точки a¢1, b¢1, c¢1, s¢1. В результате получают новую горизонтальную проекцию фигуры s1a1b1c1. (см. рис. 71). Здесь определяется угол между основанием a1b1c1 и плоскостью V – угол a°.
Из точки S1 опускается перпендикуляр на линию b1c1. Точка К1 – основание перпендикуляра. Определяется расстояние от точки S1 до плоскости основания – L1.
Определяется фронтальная проекция точки К: из точки S¢1 опускается перпендикуляр на линию a¢1d¢1. Через точку К1 проводится линия, параллельная a¢1d¢1. Пересечение линий определяет точку К¢1. Определяется положение точки К на исходной фронтальной проекции. Проводятся две дуги окружностей. Одна окружность с центром в точке а¢ и радиусом R1 = a¢1k¢1, вторая – с центром в точке b¢ и радиусом R2 = b¢1k¢1. Пересечение дуг окружностей определяет точку К¢ (см. рис. 71).
Из точки К¢ опускается перпендикуляр на ось Х. Из точки К1 проводится линия, параллельная оси Х. Пересечение линий определит горизонтальную проекцию точки К.
Выбирается новый полюс фигуры SABC. За него принимается точка b1. На горизонтальной проекции точка b1 перемещается в положение b2
параллельно оси Х. Фигура поворачивается вокруг точки b2 до положения, когда линия b2 с2 станет параллельной оси Х. (см. рис. 71).
Строится новая фронтальная проекция фигуры: через точки a¢1, b¢1, c¢1 проводятся линии параллельные оси Х (траектории движений точек). На эти линии проецируются соответствующие точки s, a, b, c . В результате получают проекцию фигуры - s¢2a¢2b¢2c¢2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.