Кафедра ИУС
Лекции по предмету
"Теория информации"
Мурыгин А. В.
Красноярск 2002
Всякий организм, в том числе и общ-й скрепляется наличием средств использования, хранения и передачи информации. Очень мало стабилизирующих процессов.
Теория информации развивалась как наука в конце 40-х г.г. В её основу положены труды Шеннона, Винера, Колмогорова, Котельникова. Это полуматематическая наука, т.е. прикладное приложение к математике.
Важным вопросом в теории информации является установленные меры информации. В качестве меры информации выделяют структурные и статические меры. Структурные меры рассматривают дискретное строение массивов информации и измеряют информацию подсчётом числа возможных информационных измерений. Статические методы учитывают вероятность появления информационных символов и в качестве меры информации используют понятие энтропия – мера неопределённости состояния систем.
Структурные методы имеют дело с информационными массивами. Массив информации представим в виде кубика.
|
|||
|
|||
а число определено.
|
|||
|
Все ячейки называются числовой грядой (один слой). Совокупность слоев – это поле.
Количество
чисел, которое может быть представлено с помощью одной числовой гряды: ![]()
В 1928г американец Хартли предложил
использовать логическую меру:![]() - это мера информации
по Хартли (аддитивная мера по Хартли) количество информации, измеренное такой
мерой, измеряется в битах (это название даёт основание log2).
Если глубина числа m = 2 – это двоичная мера информации (0
или 1), если m = 1, то кол-во информации равно один
бит. Это соответствует одному элементарному событию.
- это мера информации
по Хартли (аддитивная мера по Хартли) количество информации, измеренное такой
мерой, измеряется в битах (это название даёт основание log2).
Если глубина числа m = 2 – это двоичная мера информации (0
или 1), если m = 1, то кол-во информации равно один
бит. Это соответствует одному элементарному событию.
Обычно элементы сообщений не равновероятны, и это обстоятельство влияет на количество переданной информации. Пусть имеется алфавит из m элементов h1, h2, …,hm – элементы алфавита. Вероятности появления символов равны p1, p2, …,pm. Составим из этих элементов сообщения, содержащее n элементов. Среди них будут n1 элементов h1, n2 элементов h2, … nm элементов hm .
Предположим, что появление каждого элемента независимое событие. Тогда вероятность появления определённой комбинации выражается произведением единичных вероятностей отдельных элементов и эту вероятность можно записать:
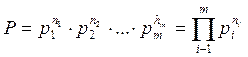
При достаточно большой длине числа n, можно считать, что ni определяется как pi*n. Кроме того можно считать, что все сообщения равновероятны, тогда вероятность отдельного сообщения:
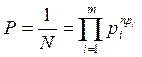 N – количество переданных сообщений;
N – количество переданных сообщений;
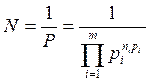
I = log2N – количество информации =
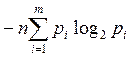
Кол-во информации, отнесённое к одному символу
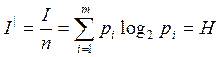 - энтропия
- энтропия
Такая мера информации была введена Шенноном. Количество информации по Шеннону определяется как I. Измеряется [бит/символ]. Она характеризует количество переданной информации при неравновероятности появления символов и характеризует неопределённость состояния сообщения.
Рассмотрим некоторую систему, которую обозначим за X, котороя может принимать конечное множество состояний x1, x2, …,xn (пример: алфавит x1,..,xn - буквы). Вероятность появления символов p1, p2, .. ,pn.
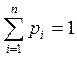
Свойства:
1) Энтропию системы X - 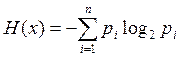 - всегда больше нуля. Это следует из
того, что log2 pi – отр., pi меньше
единицы и – на - , даёт плюс.
- всегда больше нуля. Это следует из
того, что log2 pi – отр., pi меньше
единицы и – на - , даёт плюс.
2) Энтропия обращается в 0, когда одно из состояний достоверно, а другие невозможны, т.е. какая-то из вероятностей будет равна единице, логорифм даст ноль, следовательно, Н(x) = 0.
3) Обращается в максимальное, когда все состояния равновероятны.
4) Энтропия обладает свойством аддитивности, кода несколько систем объединяются в одну, их энтропии складываются.
Рассмотрим простейший случай. Система имеет два состояния и эти состояния равновероятны.
|
|
x1 |
x2 |
||
|
p1 |
0.5 |
0.5 |
Определить энтропию системы X, которая имеет n равновероятных состояний
|
|
x1 |
x2 … |
xn |
||
|
pi |
|
|
|
- это частный случай, когда все вероятности одинаковы.
Пример: Система X имеет восемь состояний. Определить энтропию. (состояния равновероятны)
n = 8 ![]()
![]()
![]()
![]()
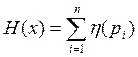
Пример: Определить H, состояние которой описывается таблицей.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.