Рекомендовано к изданию учебно-методическим советом КамчатГТУ (протокол № от ).
ÓКамчатГТУ, 2011
ÓИльина, 2011
ÓЧермошенцева, 2011
Общая характеристика дисциплины
Наряду с традиционными разделами алгебры, геометрии и математического анализа современному инженеру необходимы знания по специальным главам математических дисциплин. Особое значение приобрело изучение теории функций комплексного переменного. Функции комплексного переменного находят себе многочисленные приложения. С одной стороны, в различных прикладных математических дисциплинах (теоретическая физика, гидродинамика, теория упругости, анализ радиотехнических схем), с другой стороны, в различных разделах чистой математики (алгебра, аналитическая теория чисел, дифференциальные уравнения и пр.).
Цели и задачи дисциплины, ее место в учебном процессе
Целью дисциплины является обучение студентов современным методам анализа и синтеза, формирование у будущих специалистов умения применять математические модели взаимодействующих объектов различной природы, элементы теории оптимального управления, основы теории случайных процессов при управлении современными техническими системами, освоении методов математического моделирования, анализа технических систем и сигналов.
Основная задача курса заключается в развитии у студентов современных форм математического мышления, умения ставить и решать сложные инженерные задачи, возникающие в профессиональной практике.
В результате освоения теоретического материала, выполнения практических работ и закрепления навыков студенты должны:
ЗНАТЬ: – основные понятия теории систем применяемые для решения сложных инженерных задач.
ПОНИМАТЬ: – основные факты, понятия, определения и теоремы, алгоритмы решения типовых задач.
УМЕТЬ: – применять теоретические знания для решения практических задач, применять алгоритмы, выполнять основные математические расчеты.
Содержание дисциплины.
1. Понятие комплексного числа. Геометрическая интерпретация. Формы комплексных чисел: алгебраическая, тригонометрическая и показательная. Переход от одной формы комплексного числа к другой. Действия над комплексными числами в алгебраической, тригонометрической и показательной формах.
2. Понятие функции комплексного переменного. Дифференцируемость и аналитичность функции комплексного переменного. Условия Коши-Римана. Производная функции комплексного переменного.
3. Интегрирование функции комплексного переменного. Интегральная теорема Коши. Интеграл типа Коши. Вычисление производных функции комплексного переменного. Производные высших порядков.
4. Представление аналитических функций рядами. Ряд Тейлора. Ряд Лорана.
5. Классификация особых точек. Вычеты. Теоремы о вычетах.
Общие методические указания по изучению курса.
Основной формой обучения студентов-заочников является самостоятельная работа над учебным материалом, включающая в себя изучение материала по учебникам, решение задач, самопроверка и выполнение контрольных работ. В помощь студентам университет организует чтение лекций и проведение практических занятий.
Кроме того, студент может обращаться к преподавателю с вопросами для получения консультации. Лекции и практические занятия носят преимущественно обзорный характер. Их цель – обратить внимание на общую схему построения соответствующего раздела курса, подчеркнуть важнейшие места, указать главные практические приложения теоретического материала. На этих занятиях более подробно рассматриваются отдельные вопросы программы.
Методическое пособие содержит рекомендации по самостоятельному изучению основных вопросов курса, а также указания к выполнению отдельных заданий. Завершающим этапом изучения курса «Теория функции комплексного переменного» является сдача зачета в соответствии с учебным планом. При подготовке к зачету рекомендуется ориентироваться на вопросы итогового контроля знаний.
Вопросы для итогового контроля знаний (зачет)
1. Комплексные числа. Геометрическая иллюстрация. Формы комплексных чисел: алгебраическая, тригонометрическая и показательная.
2. Переход от одной формы комплексного числа к другой.
3. Действия над комплексными числами в алгебраической, тригонометрической и показательной формах.
4. Понятие функции комплексного переменного.
5. Дифференцируемость и аналитичность функции комплексного переменного.
6. Условия Коши-Римана. Производная функции комплексного переменного.
7. Интегрирование функции комплексного переменного.
8. Интегральная теорема Коши.
9. Интеграл типа Коши.
10. Вычисление производных функции комплексного переменного. Высшие производные.
11. Представление аналитических функций рядами.
12. Ряд Тейлора.
13. Ряд Лорана.
14. Классификация особых точек.
15. Вычеты. Теоремы о вычетах.
Типичные задания курса
Для лучшего освоения дисциплины «Теория функции комплексного переменного» и успешной сдачи зачета, рассмотрим типичные задачи изучаемого курса.
Задание №1. Даны два комплексных числа, записанных в алгебраической форме z1 = 5 + 2 i и z2 = 3 – 4 i. Найти:
а) z1+ z2; б) z1– z2
в) z1 × z2; г) z1: z2,
Решение:
а) z1+ z2 = (5 + 2 i) +(3 – 4 i) = 8 – 2 i
б) z1– z2= (5 + 2 i) – (3 – 4 i) = 2 +6 i
в)z1 × z2 = (5 + 2 i) +(3 – 4 i) = 15 – 20 i + 6 i – 8 i2.
Учитывая, что i2= – 1, получим z1 × z2 = 23 – 14 i
г)
![]() =
= ![]() . Умножим числитель и
знаменатель на сопряженное знаменателю комплексное число (3 + 4 i),
получим:
. Умножим числитель и
знаменатель на сопряженное знаменателю комплексное число (3 + 4 i),
получим:
![]() =
=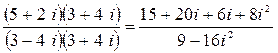 =
= ![]() = 0.28 + 1.04i.
= 0.28 + 1.04i.
Задание №2. Записать
число 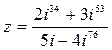 в алгебраической форме.
в алгебраической форме.
Решение:
Воспользуемся тем, что
i4×k = 1 i4×k +1 = i
i4×k +2 = i2 = –1 i4×k +3 = i3 = – i, тогда
i 34 = i4×8 +2 = i2 = –1,
i53 = i4×13 +1 = i,
i76 = i4×19 = 1, поэтому заданное число z принимает вид:
![]() .
.
Аналогично заданию 1(г) умножим числитель и знаменатель на сопряженное знаменателю комплексное число
(– 4 – 5 i), получим:
z =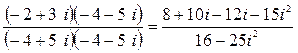 =
= ![]() =
= ![]() –
– ![]() i
i
Задание №3. Представить числа в тригонометрической и показательной форме.
а) z = – 5 + 5 i б) z = 3 i
Решение:
а) Найдем модуль комплексного числа z:
r= ïzç= ![]() =
= ![]() = 5
= 5![]() .
.
Из
соотношений cosj = 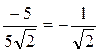 и sinj =
и sinj = 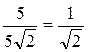 ,
получаем аргумент числа z (берем главное значение аргумента): j =
,
получаем аргумент числа z (берем главное значение аргумента): j = ![]() . Тогда z
= 5
. Тогда z
= 5![]() (cos
(cos![]() +i sin
+i sin![]() ) – тригонометрическая
форма комплексного числа. Запишем показательную форму комплексного числа: z
= 5
) – тригонометрическая
форма комплексного числа. Запишем показательную форму комплексного числа: z
= 5![]()
![]()
б) Аналогично, модуль комплексного числа z:
r= ïzç= ![]() = 3, cosj =
= 3, cosj = ![]() = 0 и sinj =
= 0 и sinj = ![]() = 1, получаем Arg z= j =
= 1, получаем Arg z= j = ![]() , т.е. z = 3 (cos
, т.е. z = 3 (cos![]() +i
sin
+i
sin![]() ) – тригонометрическая
форма комплексного числа и z = 3
) – тригонометрическая
форма комплексного числа и z = 3![]() – показательная форма
комплексного числа.
– показательная форма
комплексного числа.
Задание №4. Даны два
числа z1 = 5 (cos![]() + isin
+ isin![]() )
)
и z2= 3 (cos![]() + isin
+ isin![]() ),
записанные в тригонометрической форме. Найти: а) z1× z2; б)
),
записанные в тригонометрической форме. Найти: а) z1× z2; б)
![]() ;
;
в) z17; г)
![]() .
.
Решение:
а) Так как при умножении комплексных чисел, записанных в тригонометрической форме, их модули перемножаются, а аргументы складываются, получаем:
z1× z2 = 5×3×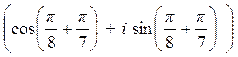 =
=
= 15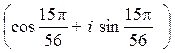 .
.
б) При нахождении частного двух комплексных чисел, записанных в тригонометрической форме модуль полученного числа равен частному модулей этих чисел, а аргумент равен разности их аргументов.
![]() =
= ![]()
 =
=
=![]()
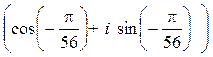 .
.
в) Для возведения числа z1 в седьмую (натуральную) степень, применим формулу Муавра:
[r (cosj + i sinj)]n = rn (cosnj + i sinnj).
Получим:
z17= 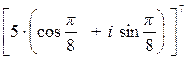 = 57
= 57 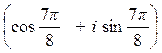 .
.
г) Для извлечения корня из комплексного числа используем формулу:
![]()
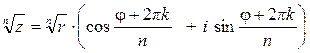 , где k
= 0, 1,…,(n –
1).
, где k
= 0, 1,…,(n –
1).
Далее при k = n, п + 1,… значения будут повторяться. Таким образом, корень п-ой степени из комплексного числа (не равного нулю) имеет п различных значений.
Имеем:
![]() =
=![]()
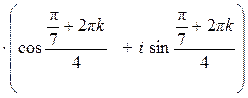 ,
где k = 0, 1, 2 и 3.
,
где k = 0, 1, 2 и 3.
Откуда получаем четыре значения корня:
при
k = 0 получаем ![]()
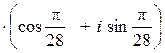 ,
,
при
k = 1 получаем ![]()
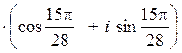 ,
,
при
k = 2 получаем ![]()
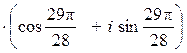 ,
,
при
k = 3 получаем ![]()
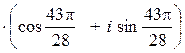 .
.
На комплексной плоскости найденные значения корня представляют
равноотстоящие друг от друга точки, расположенные на окружности радиуса ![]() , т.е. соответствуют вершинам правильного
четырехугольника (квадрата) вписанного в окружность радиуса
, т.е. соответствуют вершинам правильного
четырехугольника (квадрата) вписанного в окружность радиуса ![]() с центром в начале координат.
с центром в начале координат.
Задание №5. Изобразить множество точек комплексной плоскости, удовлетворяющих отношениям:
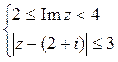
Решение:
Поскольку z = х + у i, тогда условие 2 £ Im z< 4, эквивалентно неравенству 2 £ у < 4 и задает бесконечную горизонтальную полосу между прямыми у = 2 и у = 4, включая нижнюю прямую у = 2 (рис.1).
Условие çz– (2 + i)ï£ 3 задает круг с центром в точке (2; 1) и радиусом равным 3, включая ограничивающую его окружность (рис.2).
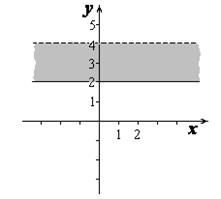
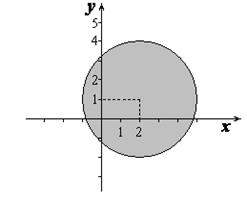
рис.1. рис.2.
Тогда получаем множество точек комплексной плоскости, удовлетворяющих заданным отношениям (рис.3).
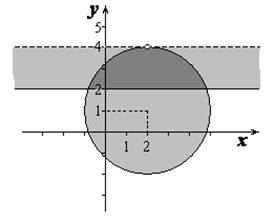
рис.3.
Задание №6. Для функции f(z)= (`z)2 найти действительную Re(f(z)) и мнимую Im(f(z)) части.
Решение:
Полагая z = х + у i, получим `z = х – у i, тогда
f(z)= (`z)2 =(х – у i)2 = х2 –2 х у i + (у i)2 = (х2– у2) + (– 2 х у)i,
откуда имеем: Re(f(z)) = (х2– у2) и Im(f(z)) = – 2 х у.
Задание №7. Показать, что функция f(z) = z2 + ziявляется аналитической. Найти производную этой функции.
Решение:
Напомним определение аналитической функции:
Определение. Функция f(z) называется аналитической (иначе, регулярной или голоморфной) в области D, если она однозначно определена и дифференцируема в каждой точке этой области.
Таким образом, для выяснения аналитичности функции необходимо
проверить выполнение условий Коши-Римана (условия дифференцируемости функции): 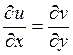 и
и 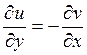 , где и(х, у)
– действительная часть функции комплексного переменного и v(х,
у) – мнимая.
, где и(х, у)
– действительная часть функции комплексного переменного и v(х,
у) – мнимая.
Функция f(z) = z2 + zi, всюду определенная на комплексной плоскости и т.к. z = х + у i, получаем:
f(z) = z2 + zi = (х + у i)2 + (х + у i)×i = (х2 – у2 – у) + (2х у +х) i, т.е.
и(х, у) = х2 – у2 – у v(х, у) = 2х у +х.
Найдем частные производные действительных функций
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.