Интерполирование кубическими сплайнами.
Пусть
задан набор узлов ![]() , который мы будем называть сеткой.
Величину
, который мы будем называть сеткой.
Величину ![]() мы будем называть шагом сетки.
Кубический интерполяционный сплайн на интервале
мы будем называть шагом сетки.
Кубический интерполяционный сплайн на интервале ![]() с сеткой
с сеткой ![]() - это функция
- это функция ![]() удовлетворяющая следующим условиям:
удовлетворяющая следующим условиям:
1)
![]() - полином третьей степени на каждом
из подинтервалов
- полином третьей степени на каждом
из подинтервалов ![]()
2)
![]()
3)
![]()
Для построения такого сплайна ![]() нужно определить 4n
неизвестных величин- по 4 коэффициента полинома третьей степени на каждом из n
нужно определить 4n
неизвестных величин- по 4 коэффициента полинома третьей степени на каждом из n
В нашем распоряжении имеются:
3(n-1)
условий непрерывности самой функции S(x),
её первой и второй производных во внутренних узлах ![]()
(n+1)
условие интерполяции ![]()
Таким образом, для определения 4n
неизвестных величин мы имеем всего ![]() условий. Недостающие условия
определяют различными способами, среди которых могут быть задание на концах
интервала
условий. Недостающие условия
определяют различными способами, среди которых могут быть задание на концах
интервала ![]() первой или второй производной,
либо условия периодичности.
первой или второй производной,
либо условия периодичности.
Будем искать кусочно-полиномиальное представление нашего кубического сплайна в виде
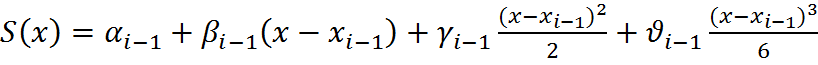
для x![]() При этом ясно, что
При этом ясно, что ![]()
Поскольку S”(x)
является линейной функцией на ![]() , то её вид полностью определяется
двумя её крайними значениями
, то её вид полностью определяется
двумя её крайними значениями ![]() на концах интервала
на концах интервала ![]() . Имеем поэтому
. Имеем поэтому
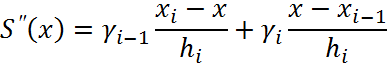
для ![]() Отметим, что в этих формулах мы
уже задействовали значения
Отметим, что в этих формулах мы
уже задействовали значения ![]() и
и ![]() второй производной S’’
на левом и правом концах интервала [a,b].
Очевидно, что построенная таким образом функция S’’(x)
удовлетворяет условию “непрерывной склейки” в узлах
второй производной S’’
на левом и правом концах интервала [a,b].
Очевидно, что построенная таким образом функция S’’(x)
удовлетворяет условию “непрерывной склейки” в узлах ![]()
Беря дважды первообразную от S’’(x), получим
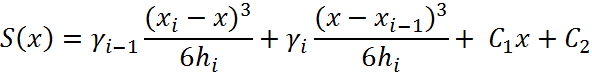
с какими-то константами ![]() и
и ![]() . Но нам будет удобно представить
это выражение в виде
. Но нам будет удобно представить
это выражение в виде
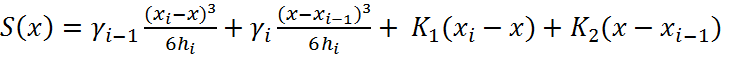
где
![]() и
и ![]() -так же константы.
-так же константы.
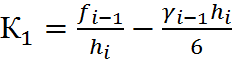
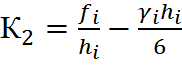
Окончательно выражение сплайна на интервале ![]()
![]() выглядит следующим образом
выглядит следующим образом
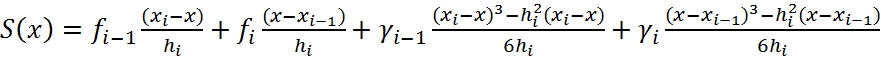
Оно не содержит уже
величин ![]() , но неизвестными остались
, но неизвестными остались ![]()
Чтобы завершить определение вида сплайна, т.е. найти
![]() , можно воспользоваться условием
непрерывности первой производной S’(x)
в узлах
, можно воспользоваться условием
непрерывности первой производной S’(x)
в узлах ![]() :
:
![]()
![]() .
.
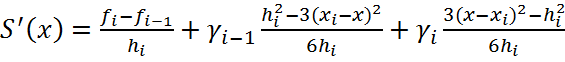 ;
;
Продифференцировав последние формулы и приравняв производные, полученные для узлов интерполирования с соседних подинтервалов-слева и справа, будем иметь систему уравнений
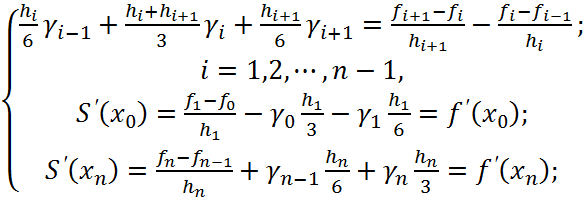
Это система линейных алгебраических уравнений
относительно неизвестных переменных ![]() , c
трёхдиагональной матрицей
, c
трёхдиагональной матрицей
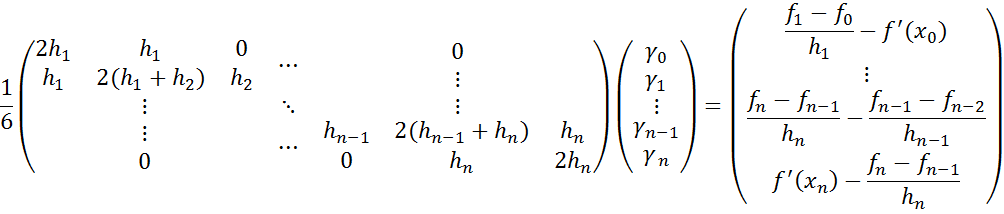
СЛАУ с трехдиагональной матрицей решаются методом прогонки:
Система уравнений равносильна соотношению
![]()
Метод прогонки основывается на предположении, что искомые неизвестные связаны рекуррентным соотношением:
![]() где
где
![]()
Используя это соотношение, выразим ![]() и
и ![]() через
через ![]() и подставим в уравнение (1):
и подставим в уравнение (1):
![]() ,
,
где ![]() — правая часть i-го уравнения. Это
соотношение будет выполняться независимо от решения, если потребовать
— правая часть i-го уравнения. Это
соотношение будет выполняться независимо от решения, если потребовать
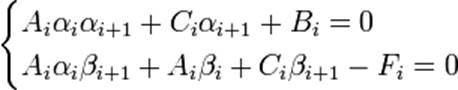
Отсюда следует:
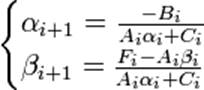
Из первого уравнения получим:
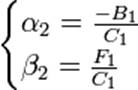
После нахождения прогоночных коэффициентов α и β, используя уравнение (2), получим решение системы. При этом,
![]()
![]()
Получили:
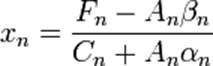
Методом прогонки нашли значения коэффициентов ![]() , i=0,1,…,n.
, i=0,1,…,n.
Подставляем их в
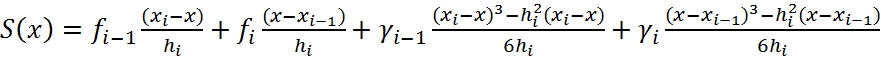 ;
;
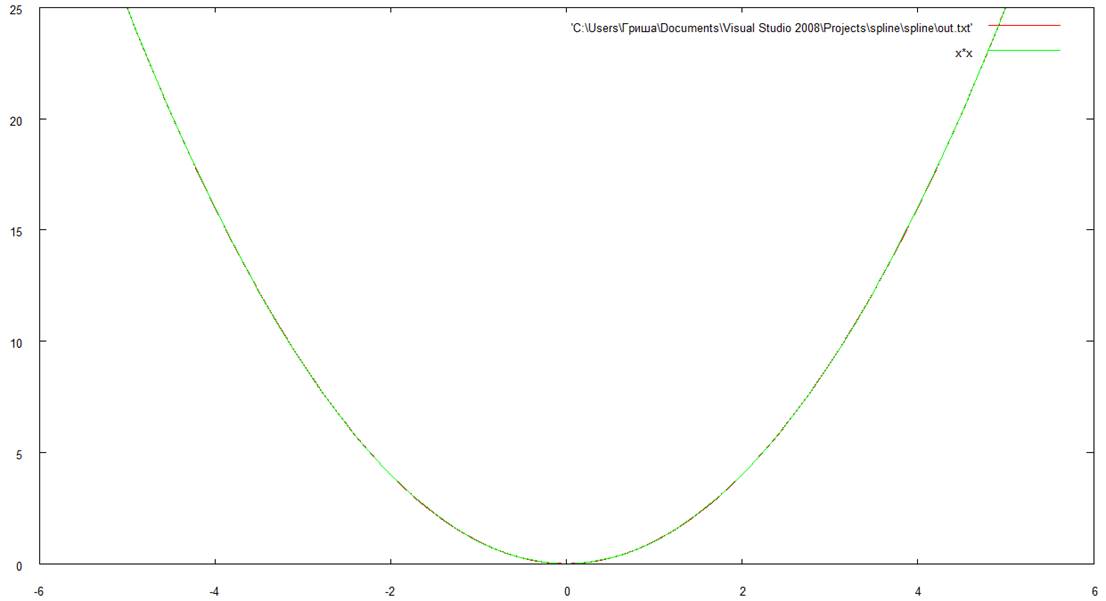
Для построения более точного графика кубического
сплайна будем разбивать каждый ![]() на n
отрезков
и строим сплайн на каждом
на n
отрезков
и строим сплайн на каждом ![]()
Строим график сплайна для функций:
1.
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.