НЕЧІТКЕ ВИВЕДЕННЯ (НВ)
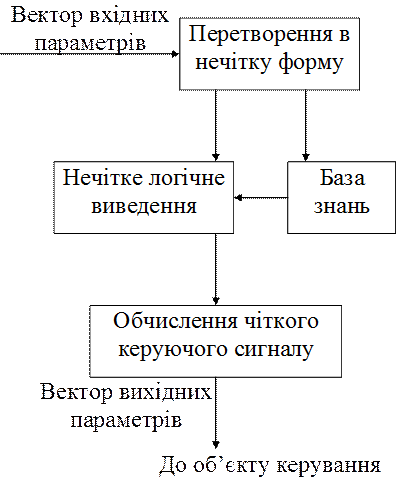 Структура НВ
складається з фазифікації (перетворення вхідних сигналів у нечітку форму),
формування нечіткого логічного висновку, дефазифікації (формування чіткого
керуючого висловлення).
Структура НВ
складається з фазифікації (перетворення вхідних сигналів у нечітку форму),
формування нечіткого логічного висновку, дефазифікації (формування чіткого
керуючого висловлення).
Фазифікація:
Потрібна тому, що вхідні параметри існують у різних чітких формах (частина у формі, природної для користувача, частина з датчиків). Змінні за певними правилами повинні бути перетворені в значення функції належності μ(p), які повинні мати єдиний діапазон змінювання (найчастіше це [0..1]). Щоб задовольнити останній вимозі використовують масштабування:
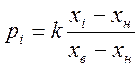 ,
,
де pi – машинна змінна, xi, xн, хв. – обмірюване, нижнє і верхнє значення діапазону зміни сигналу, k- коефіцієнт.
На підставі машинних змінних обчислюються значення функції належності μ(p).
припустимо, що нечіткі множини (НМн), які беруть учать в операції, задані на ділянці визначення з однаковим кроком Δ, тобто
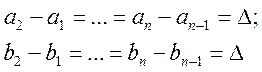
Ефективність застосування подібних моделей, формованих експертами на основі особистого досвіду, багато в чому залежить від кількості термів і використовуваних лінгвістичних змінних (ЛЗ) і від виду відповідних функцій належності. ЛЗ повинні мати терм –множину, що складається з 2-12 елементів, де два елементи потрібні для опису двійкових об’єктів.
Функції належності,
що використовуються для опису терм-множини T={Ti}, i![]() L{1..m}, деякої ЛЗ i з
ділянкоюU
L{1..m}, деякої ЛЗ i з
ділянкоюU![]() R визначення на множині дійсних чисел,
через свою семантику повинні формуватися з урахування специфічних вимог:
R визначення на множині дійсних чисел,
через свою семантику повинні формуватися з урахування специфічних вимог:
|
|
(1) |
|
(2) |
|
|
(3) |
Формування нечіткого логічного висновку:
Основним інструментом є композиція – операція над нечіткими відношеннями:
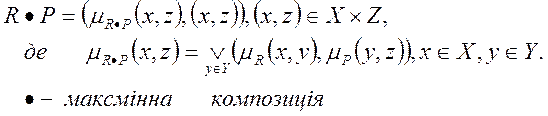
Для лігвістичної
моделі сукупність продукційних правил задає деяке відображення множини вхідних
лінгвістичних змінних (ЛЗ) в множину вихідних: ![]() , де
, де ![]() ,
, ![]() . Чому
можна поставити у відповідність нечітке відображення
. Чому
можна поставити у відповідність нечітке відображення
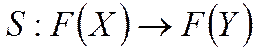 , де
, де 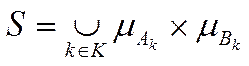 ,
, 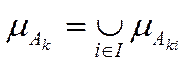 ,
, 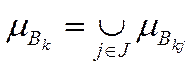 .
.
Тоді з правила modus ponens (з класичної логіки: Посилання 1: ЯКЩО Х є А, ТО Y є C. Посилання 2: Х є A. Висновок: Y є C.) можна отримати композиційне правило для нечіткої логіки:
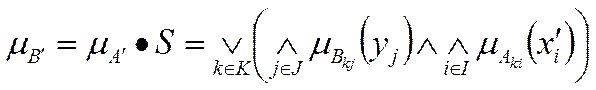
де ![]() - вихідне посилання, отримане фазифікацією
вхідних даних,
- вихідне посилання, отримане фазифікацією
вхідних даних, ![]() - нечіткий результат логічного
виведення (А’ і В’ – твердження близькі до А і В відповідно) .
- нечіткий результат логічного
виведення (А’ і В’ – твердження близькі до А і В відповідно) .
Приклад: Дано нечітке правило "ЯКЩО x=![]() , ТО у=
, ТО у=![]() " з нечіткими множинами:
" з нечіткими множинами:
![]() ={(0, 1), (0.1, 2), (0.5, 3), (0.8, 4),
(1, 5)} та
={(0, 1), (0.1, 2), (0.5, 3), (0.8, 4),
(1, 5)} та ![]() = {(1, 5),
(0.8, 10), (0.4, 15), (0.2, 20)}.
= {(1, 5),
(0.8, 10), (0.4, 15), (0.2, 20)}.
Розрахувати
значення вихідної змінної у, якщо x=![]() = {(0.3, 1), (0.5, 2), (1, 3), (0.7, 4), (0.4, 5)}.
= {(0.3, 1), (0.5, 2), (1, 3), (0.7, 4), (0.4, 5)}.
Спочатку розрахуємо
нечітке відношення, що відповідає правилу " ЯКЩО x=![]() , ТО у=
, ТО у=![]() ":
":
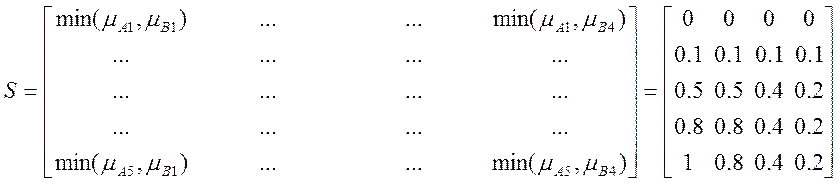
Тепер, по формулі ![]() розрахуємо нечітке значення вихідної
змінної:
розрахуємо нечітке значення вихідної
змінної:
у = {(![]() , B1),()...(),(
, B1),()...(),(![]() , B4)}=
, B4)}=
={(0.7, 5), (0.7, 10), (0.4, 15), (0.2, 20)}
Дефазифікація:
Процедура перетворення НМн в чітке число а (чітке керуюче висловлювання), аналог знаходження характеристик положення (математичного очікування, моди, медіани) випадкових величин в теорії ймовірності. Найпростішим способом виконання процедури дефазифікації є вибір чіткого числа, що відповідає максимуму функції належності. Але застосування цього способу можливе лише для одноекстремальних функцій належності. Для багатоекстремальних функцій належності використовуються такі методи дефазифікації:
а) “центру ваги” 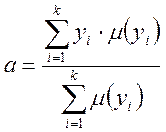
Фізичним аналогом даної формули є знаходження центру ваги плоскої фігури, обмеженої осями координат і графіком функції належності.
б) “медіани” 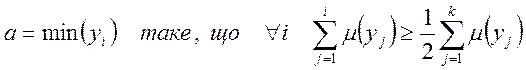
Геометричною інтерпретацією метода медіани є знаходження такої точки на оси абсцис, що перпендикуляр, проведений в цій точці, поділяє площину під кривою функції належності на дві рівні частини.
в) “центру максимумів”, за яким знаходиться середнє арифметичне елементів універсальної множини G, які мають максимальні ступені належностей.
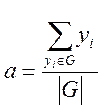 ,
,
де ![]() - потужність множини G.
- потужність множини G.
Приклад: Провести дефазифікацію нечіткої множини ![]() = {(0.3, 1), (0.5, 2), (1, 3), (0.7, 4), (0.4,
5)}. по методу центру ваги.
= {(0.3, 1), (0.5, 2), (1, 3), (0.7, 4), (0.4,
5)}. по методу центру ваги.
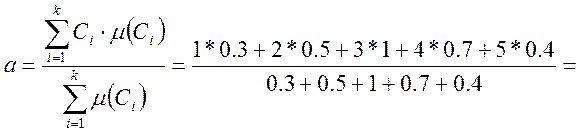 3,66.
3,66.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.