VI.Функциимногихпеременных.
Предел функции: X и Y – метрические пространства. E из X, f:E->Y. p –
предельная точка Е. Будем обозначать ![]() ,
если $ q Î Y: " ε>0 $ б>0: ρy(f(x),q)<ε => ρx(x,p)<б
,
если $ q Î Y: " ε>0 $ б>0: ρy(f(x),q)<ε => ρx(x,p)<б
Свойства пределов: 1)![]() 2) lim(f(x)g(x))=ab 3)lim(f(x)/g(x))=a/b
2) lim(f(x)g(x))=ab 3)lim(f(x)/g(x))=a/b
Непрерывность функции многих переменных:
X и Y – метрические пространства. E из X, f:Х->Y. p – предельная точка Е. Функция f называется непрерывной в точке p, если " ε>0 $ б>0: ρx(f(x),f(p))<ε . " x: ρx(x,p)<б
Локальные свойства: 1) Пусть р - изолированная точка. Тогда " f, определенных на множестве Х в точке р будет непрерывной в этой точке. 2)Пусть р – предельная точка Х. f непрерывна в р ó когда lim(f(x))=f(p). 3) Отображение f:X->Rm непрерывно в некоторой точке p Î Х, ограничено в некоторой точке р Î Х, ограничено в некоторой окрестности этой точки. 4) Если отображение g: Y->Rk, Y из Rm, непрерывно в точке y0 Î Y и отображение f:X->Y, X из Rm непрерывно в точке x0 Î Х, причем f(x0)=y0, то определено отображение h(x)=g(f(x)). H:X->Rk. h – суперпозиция отображений. 5) Если вещественнозначная функция f: X->R непрерывна в точке p Î Х и f(p)>0 (f(p)<0), То найдется такая окрестность точки p, что " x Î U(p) f(x)>0(<0). 6) Если f,g: X->R непрерывны в точке p Î X, то их линейная комбинация (αf+βg);fg;f/g будут непрерывны в точке p.
Равномерная непрерывность: f:X->Rm , X Î Rn называется равномерно непрерывным на Х, если " ε >0 $ б>0: " x1,x2 Î Х, ρ(x1,x2)<б => ρ(f(x1),f(x2))<ε
Условие Гельдера(Липшица) порядка α (0<α≤1). $ K: " x1,x2 Î Х ρy(f(x1),f(x2))≤k[ρx(x1,x2)]α
f(компакта) = компакт
Глобальные свойства:
1)Если отображение f:X->Rn, где Х-подмножество Rn, непрерывно на компакте Х, то оно равномерно непрерывно на нем. 2) Если отображение f:X->Rn, где Х-подмножество Rn, непрерывно на компакте Х, то оно ограничено на Х. 3) Если отображение f:X->R, где Х-подмножество Rm, непрерывно на компакте Х, то она принимает мин. и макс. значение на нем 4)Если функция f:X->R непрерывна на связном множестве Х и принимает в точках a,b значения А=f(a), B=f(b), то для " С:A<C<B $ сÎХ, f(c)=C;
Полное метрическое пространство: Метрическое пространство Х называется полным, если " последовательность Коши сходится к элементу этого пространства.
Пусть в метрическом пространстве Х задана последовательность точек x0,x1,…,xn, которая сходится к некоторой точке х, тогда эта последовательность будет обладать свойством: " ε>0: $ N:" n,m>N: ρ(xn,xm)<ε и называется фундаментальной или последовательностью Коши.
Теорема о неподвижной точке: f:X->X называется сжатием или сжимающим отображением, если $ 1>k>0, что для " пары элементов из Х: ρ(f(x),f(y))≤kρ(x,y). Тогда оно удовлетворяет условию Липшица и равномерно непрерывно. Т.а Î Х называется неподвижной точкой отображения Х, если выполняется f(a)=a;
Т. Каждое сжатие полного метр. простр-ва имеет неподвижную точку и при том единственную.
Дифференцируемость и дифференциал функции в точке
F:X->Rn, х Î Rm,
называется дифференциалом в точке х множества Х, где х-некоторая предельная
точка множества Х. если выполняется следующее равенство (1)f(x+h)-f(x)=L(x)h+α(x;h),
где L(x):Rm->Rn (линейна относительно h), α(x;h)=o(h)при
h->0, h-малая величина;Δx(h)=(x+h)-x = h – приращение
аргумента; Δf(x(h))=f(x+h)-f(x) называется приращением функции и обозначается Δx и Δf.
Линейная функция L(x): Rm->Rn называется дифференциальным касательным
отображением или производным отображением функции f:X->Rn . Дифференциал f
обозначается так: df(x), Дf(x),. или ![]() , тогда формула 1
выглядит так: f(x+h)=f(x)=
, тогда формула 1
выглядит так: f(x+h)=f(x)= ![]() h+o(h)
h+o(h)
Частные производные: x0 – нулевой элемент пространства. Если все векторы 1 f(x+h),f(x),L(x)h,α(x;h)h из
пространства Rn записать в покоординатной форме, то равенство 1
тождественно равенствам: ![]()
Лемма1: Отображение F:X->Rn, X Î Rm дифференцируемо в предельной точке х множества Х ó в этой точке дифференцируемы все вещественнозначные функции fi
Лемма2: Если функция F:X->R, X Î Rm, дифференцируема во внутренней точке множества Х, то
функция имеет частные производные по каждой переменной и дифференциал функции
однозначно определяется частными производными в следующем виде(8).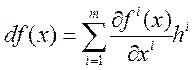 , (9)
, (9)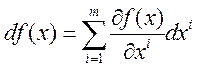
Непрерывность. Дифференцируемость функции в точке и частные производные. Поскольку в 1, L- линейный оператор, то Lh->0, таким образом из 1: функция дифференцируемая в точке непрерывна в этой точке. Обратное утверждение неверно.
Основные свойства дифференцирования:
Т1. Пусть дана f1:X->Rn ,
f2:X->Rn и они дифференцируемы в точке х Î Х. Тогда их
линейная комбинация также дифференцируема в этой точке, причем для нее
выполняется равенство: ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.