Новосибирский Государственный Технический Университет
Лабораторная работа №3 по курсу
“Уравнения математической физики”
|
Факультет: Группа: Студенты: Преподаватели: |
ПМИ ПМ-51 Саяпина М.А. Шмидт Е.В. Задорожный А.Г. |
1. Цель работы
Разработать программу решения гармонической задачи методом конечных элементов. Сравнить прямой и итерационный методы решения получаемой в результате конечноэлементной аппроксимации СЛАУ.
2. Теоретическая часть
Рассмотрим уравнение:
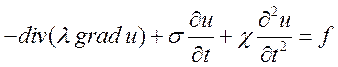
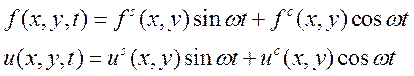
Базисные функции билинейные.
2. Вывод формул
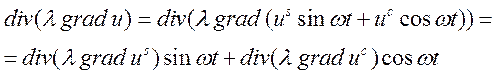
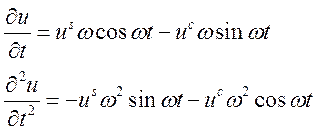
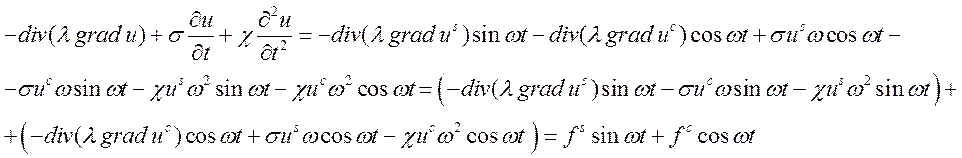
Приравняв значения при синусах и косинусах, получим систему из 2-х уравнений:
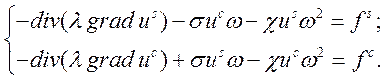
Учитывая, что 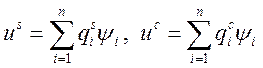 получаем:
получаем:
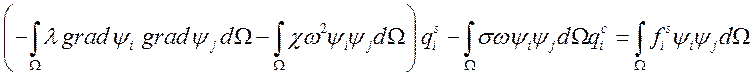
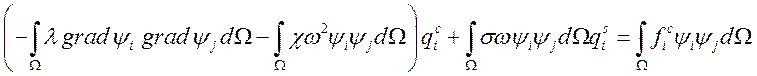
Обозначим через
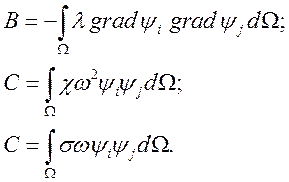
и, представив вектор неизвестных в виде ![]() , получим матрицу вида:
, получим матрицу вида:
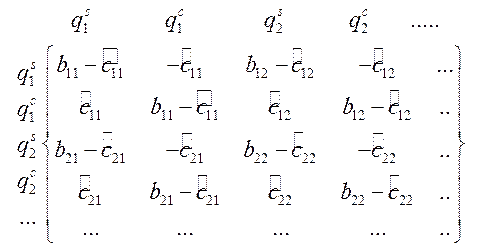
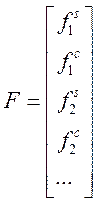
Для того, чтобы построить вышеописанную матрицу воспользуемся уже вычисленными матрицами жесткости и массы с учетом того, что базисом являются билинейные функции:
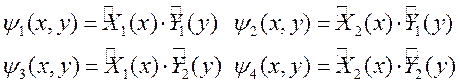
где
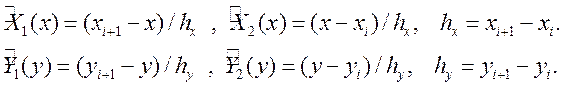
Тогда
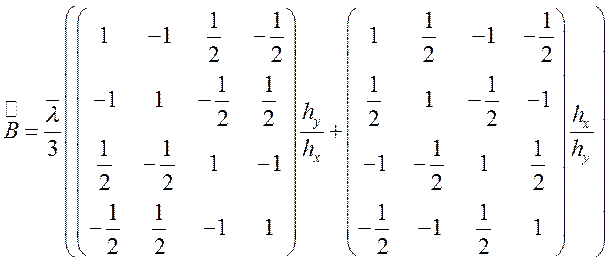
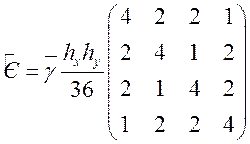
и вектор правой части:
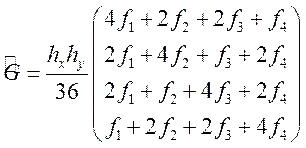
3. Текст программы
Содержимое файла L3UMF.сpp
#include "stdafx.h"
#include <stdio.h>
#include "MKE.h"
void main()
{
MKE du;
if(du.initialization(Grid)) { printf("Is not initialized\n"); return; }
else printf("Initialization\tOk.\n");
du.construction_global_SLAU();
printf("Construction\tOk.\n");
if(du.save_information())
{
printf("Is not saved\n");
return;
}
else printf("Save\t\tOk.\n");
}
Содержимое файла MKE.h
#include "files.h"
struct global_sist
{
int n, *ig, *jg; // n - размерность СЛАУ
double *ggl, *ggu, *di, *pr;
};
class MKE
{
public:
int initialization(char*); // подготовка исходных данных
void construction_global_SLAU(); // построение СЛАУ
int save_information(); // сохранение результата в форматах
private:
global_sist slau; // данные глобальной СЛАУ
double loc_m[8][8], loc_v[8]; // локальная матрица и локальный вектор
double lambda, sigma, Hi, omega, // коэффициенты уравнения
*x, *y; // разбиение сетки по x, y
int nx, ny; // количество узлов по оси x, y
void generation_ig(); // создаем массив ig
void generation_jg(); // создаем массив jg
int portret(); // создаем портрет матрицы глобальной СЛАУ
void clearing(); // очистка содержимого векторов ggl, ggu, di, pr
void definition_of_local_system(int, int); // построение локальной СЛАУ
void addition_in_SLAU(int, int); // добавление в глобальную
void conditions(); // учет краевых условий
int preservation_of_file(char*, double*, int*, int); // сохранение одного массива
void gg_gen_in_profile(FILE*, double*); // перевод матрицы (ggl, ggu) в проф. формат
};
Содержимое файла MKE.cpp
#include "stdafx.h"
#include "MKE.h"
#include "funcs.h"
#include "conditions.h"
double B1[4][4]= { 1, -1, .5, -.5,
-1, 1, -.5, .5,
.5, -.5, 1, -1,
-.5, .5, -1, 1},
B2[4][4]= { 1, .5, -1, -.5,
.5, 1, -.5, -1,
-1, -.5, 1, .5,
-.5, -1, .5, 1},
C[4][4] = { 4, 2, 2, 1,
2, 4, 1, 2,
2, 1, 4, 2,
1, 2, 2, 4 };
int MKE::initialization(char *grid)
{
int i;
for(i = 0; i < 4; i++)
for(int j = 0; j < 4; j++)
{
B1[i][j] /= 3.;
B2[i][j] /= 3.;
C [i][j] /= 36.;
}
FILE *file;
if(!(file = fopen(grid, "r")))return 1;
fscanf(file, "%d %d", &nx, &ny);
if(!(x = new double[nx]))return 2;
if(!(y = new double[ny]))return 3;
for(i = 0; i < nx; i++)
fscanf(file, "%le", x + i);
for(i = 0; i < ny; i++)
fscanf(file, "%le", y + i);
fclose(file);
FUNCS(lambda, sigma, Hi, omega);
return portret();
}
int MKE::portret()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.