12. Специальная теория относительности.
Преобразования Лоренца. Промежуток времени между событиями. Длина отрезка. Лоренцово сокращение. Четырехмерное пространство Минковского. Интервал. Собственное время. Сложение скоростей. Аберрация света. Релятивистская механика частицы. 4 – скорость. 4 – ускорение. Четырехмерное уравнение движения. 4 – импульс. Сила Минковского. Энергия частицы. Принцип эквивалентности. Движение заряженной частицы во внешнем электромагнитном поле в вакууме. Циклотронная частота. Эффект Доплера. Аберрация света. Преобразования Лоренца 4 – потенциала и 4 – тока в электродинамике. Тензор электромагнитного поля в вакууме. Тензор индукции. Релятивистская 4 – сила Лоренца. Тензорная форма уравнений Максвелла.
12.1. Преобразования Лоренца. Промежуток времени между событиями. Длина отрезка. Лоренцово сокращение. Четырехмерное пространство Минковского.
Экспериментальным
фактом является то, чтов вакууме распространяются электромагнитные
волны с определенной скоростью ![]() . Эта скорость не
зависит от выбора инерциальной системы отсчета. На первый взгляд это кажется
неверным, так как противоречит закону сложения скоростей классической механики.
Согласно этому закону, если
. Эта скорость не
зависит от выбора инерциальной системы отсчета. На первый взгляд это кажется
неверным, так как противоречит закону сложения скоростей классической механики.
Согласно этому закону, если ![]() скорость волны в
инерциальной системе отсчета
скорость волны в
инерциальной системе отсчета ![]() , то в другой
инерциальной системе отсчета
, то в другой
инерциальной системе отсчета ![]() скорость волны должна
быть
скорость волны должна
быть ![]() , где
, где ![]() -
скорость системы
-
скорость системы ![]() относительно системы
относительно системы![]() Дело в том, что необходимо отказаться от
абсолютного характера времени и от преобразования Галилея для координат в
системах отсчета
Дело в том, что необходимо отказаться от
абсолютного характера времени и от преобразования Галилея для координат в
системах отсчета ![]() и
и ![]() :
:
![]() ,
, ![]() ,
,
где
![]() - время, одинаковое в обеих системах
отсчета.
- время, одинаковое в обеих системах
отсчета.
Покажем,
что в электродинамике справедливо другое преобразование (оно называется
преобразованием Лоренца) для координат и времен событий в инерциальных системах
отсчета ![]() и
и ![]() .
Рассмотрим процесс распространения плоских электромагнитных волн в вакууме,
описывая его волновым уравнением в инерциальной системе
.
Рассмотрим процесс распространения плоских электромагнитных волн в вакууме,
описывая его волновым уравнением в инерциальной системе ![]()
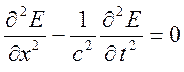 ,
,
тогда
соответствующее волновое уравнение в инерциальной системе отсчета ![]() должно иметь вид
должно иметь вид
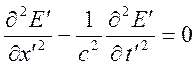 ,
,
где
учтено, что ![]() . Так как обе системы отсчета инерциальные,
то имеет место неизменность (инвариантность) волнового уравнения и
. Так как обе системы отсчета инерциальные,
то имеет место неизменность (инвариантность) волнового уравнения и ![]() . Такая связь невозможна, если справедливо
преобразование Галилея. Волновые уравнения – линейные, поэтому должно
существовать линейное преобразование координаты и времени события в виде
. Такая связь невозможна, если справедливо
преобразование Галилея. Волновые уравнения – линейные, поэтому должно
существовать линейное преобразование координаты и времени события в виде
![]() ,
,
где
![]() - некоторые константы, зависящие от
параметров, описывающих задачу (определяющих параметров)
- некоторые константы, зависящие от
параметров, описывающих задачу (определяющих параметров) ![]() (
(![]() -
относительная скорость движения систем отсчета). Первая производная по
координате
-
относительная скорость движения систем отсчета). Первая производная по
координате ![]() представляется в виде
представляется в виде
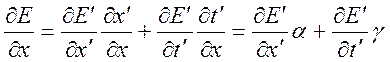 ,
,
где
учтено, что ![]() и вторые производные связаны соотношениями
и вторые производные связаны соотношениями
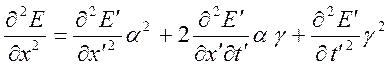 ,
,
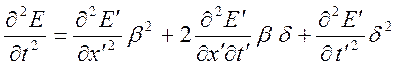 .
.
Неизменность (инвариантность) волнового уравнения при переходе в другую инерциальную систему отсчета приводит к трем условиям
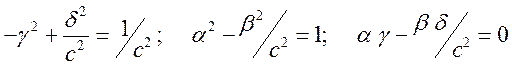 .
.
Имеет
место преобразование координаты 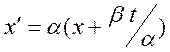 . Для того, чтобы это
новое преобразование переходило в преобразование Галилея при
. Для того, чтобы это
новое преобразование переходило в преобразование Галилея при ![]() , необходимо взять
, необходимо взять 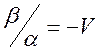 .
Следствием последнего является представление
.
Следствием последнего является представление 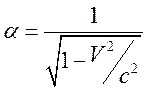 . В
результате получим получим преобразование Лоренца
. В
результате получим получим преобразование Лоренца
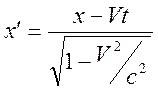 ,
, 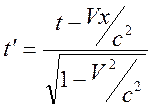 . (12.1)
. (12.1)
Принципиально
новым в преобразовании Лоренца по сравнению с преобразованием Галилея является
то, что время ![]() в системе
в системе ![]() отличается от времени
отличается от времени ![]() в системе
в системе ![]() .
Инвариантность скорости света обеспечивается в результате отказа от абсолютного
характера времени.
.
Инвариантность скорости света обеспечивается в результате отказа от абсолютного
характера времени.
Рассмотрим
два события, происходящие в точке ![]() системы
системы ![]() в моменты
в моменты ![]() и
и ![]() . В системе
. В системе ![]() в точке
в точке
![]() соответствующие моменты времени
представляются в виде
соответствующие моменты времени
представляются в виде
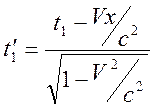 ,
, 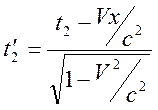
и промежутки времени между событиями в двух системах связаны соотношением
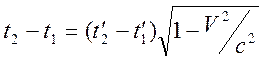 ,
,
показывающим,
что эти промежутки времени отличаются. Отметим важное обстоятельство.
Промежуток времени в системе ![]() определяется по одним
часам
определяется по одним
часам ![]() (эти часы находятся в точке
(эти часы находятся в точке ![]() ). Показания времени
). Показания времени ![]() и
и ![]() определяются
по двум различным, разнесенным в пространстве часам
определяются
по двум различным, разнесенным в пространстве часам ![]() и
и ![]() .
.
Рассмотрим
длину отрезка (стержня) в двух инерциальных системах отсчета. Пусть стержень
длиной ![]() покоится в системе
покоится в системе ![]() .
Найдем координаты
.
Найдем координаты ![]() концов этого стержня в системе
концов этого стержня в системе ![]() в один и тот же момент времени
в один и тот же момент времени ![]() . Из преобразования Лоренца имеем
. Из преобразования Лоренца имеем
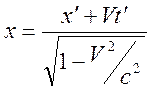 .
.
Взяв
![]() , получим связь
, получим связь
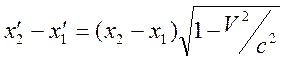 .
.
Наибольшую
длину стержень имеет в той системе отсчета, в которой он покоится. Эту длину
называют собственной длиной стержня. Уменьшение длины стержня в системе ![]() по сравнению с собственной длиной в
по сравнению с собственной длиной в 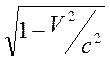 раз называют лоренцевым сокращением.
раз называют лоренцевым сокращением.
Из преобразований Лоренца следует
![]() ,
,
то
есть, величина ![]() является инвариантной. В общем
случае имеется инвариантность квадратичной формы
является инвариантной. В общем
случае имеется инвариантность квадратичной формы
![]() . (12.2)
. (12.2)
Представляется
удобным ввести четырехмерное пространство (4 - пространство)
псевдоевклидово пространство Минковского. Оно представляет совокупность точек (![]() ), где
), где ![]() (четвертая
координата является мнимой величиной). Точки в этом пространстве называют мировыми
точками. Каждой такой точке соответствует некоторое событие. Инвариантность
квадратичной формы (12.2) означает, что преобразованию Лоренца соответствует
поворот системы координат в пространстве Минковского.
(четвертая
координата является мнимой величиной). Точки в этом пространстве называют мировыми
точками. Каждой такой точке соответствует некоторое событие. Инвариантность
квадратичной формы (12.2) означает, что преобразованию Лоренца соответствует
поворот системы координат в пространстве Минковского.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.