Согласно основным положениям
макроскопической электродинамики электромагнитное поле (ЭМП) в каждый момент
времени определяется векторами ![]() и
и ![]() , характеризующими электрическое поле, и
векторами
, характеризующими электрическое поле, и
векторами ![]() и
и ![]() ,
характеризующими магнитное поле. В уравнениях ЭМП, помимо этих четырех
векторов, фигурируют еще две величины: плотность заряда
,
характеризующими магнитное поле. В уравнениях ЭМП, помимо этих четырех
векторов, фигурируют еще две величины: плотность заряда ![]() и
плотность тока
и
плотность тока ![]() ; они характеризуют источники
поля – заряды и токи, наличие которых приводит к возбуждению поля в окружающем
пространстве. Уточним: в макроскопической электродинамике
; они характеризуют источники
поля – заряды и токи, наличие которых приводит к возбуждению поля в окружающем
пространстве. Уточним: в макроскопической электродинамике ![]() есть плотность свободного электрического
заряда, а
есть плотность свободного электрического
заряда, а ![]() - плотность электрического тока (тока
проводимости). При отсутствии макроскопических перемещений вещества плотность
тока и плотность заряда связаны уравнением непрерывности:
- плотность электрического тока (тока
проводимости). При отсутствии макроскопических перемещений вещества плотность
тока и плотность заряда связаны уравнением непрерывности:
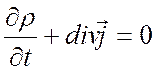 , (1.1)
, (1.1)
выражающим тот факт, что ток проводимости обусловлен движением свободных зарядов, подчиняющихся закону сохранения электричества.
Векторы ЭМП, а также величины ![]() и
и ![]() зависят
от трех пространственных координат (например, от декартовых координат x, y, z)
и времени t. Они связаны между собой системой
уравнений Максвелла:
зависят
от трех пространственных координат (например, от декартовых координат x, y, z)
и времени t. Они связаны между собой системой
уравнений Максвелла:
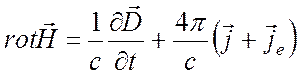 , (1.2)
, (1.2)
![]() , (1.3)
, (1.3)
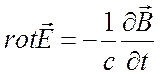 , (1.4)
, (1.4)
![]() .
(1.5)
.
(1.5)
При этом здесь и далее используется абсолютная система
единиц СГС; с – скорость света в пустоте, равная ![]() . В
уравнении (1.2) учтены также так называемые сторонние токи
. В
уравнении (1.2) учтены также так называемые сторонние токи ![]() , которые считаются заданными. Они
возбуждают поля, но сами не порождаются рассматриваемыми ЭМП, в этом смысле они
являются сторонними этому полю. Эти уравнения являются обобщением опытных
данных в дифференциальной форме. Так, уравнение (1.4) есть закон
электромагнитной индукции Фарадея, (1.2) – закон Био – Савара – Лапласа.
Уравнения (1.3) и (1.5) – законы Кулона и Гаусса соответственно, показывающие
как ЭМП возбуждается своими источниками.
, которые считаются заданными. Они
возбуждают поля, но сами не порождаются рассматриваемыми ЭМП, в этом смысле они
являются сторонними этому полю. Эти уравнения являются обобщением опытных
данных в дифференциальной форме. Так, уравнение (1.4) есть закон
электромагнитной индукции Фарадея, (1.2) – закон Био – Савара – Лапласа.
Уравнения (1.3) и (1.5) – законы Кулона и Гаусса соответственно, показывающие
как ЭМП возбуждается своими источниками.
Приведенная система уравнений справедлива для ЭМП в любых средах. Однако этих уравнений недостаточно для решения конкретных задач, ибо их число меньше числа неизвестных. Недостаточность этой системы уравнений объясняется именно ее универсальностью – она применима к ЭМП в любых средах, между тем как параметры, характеризующие среду, в ней отсутствуют. Поэтому при решении конкретных задач эти уравнения необходимо дополнить системой материальных уравнений, в которых учитывается влияние среды на протекающие в ней электромагнитные явления.
В электродинамике рассматриваются в первую очередь простейшие материальные уравнения:
![]() ,
,
![]() , (1.6)
, (1.6)
![]() ,
(1.7)
,
(1.7)
где ![]() и
и ![]() -
диэлектрическая и магнитная проницаемость среды соответственно,
-
диэлектрическая и магнитная проницаемость среды соответственно, ![]() - проводимость. Они охватывают
электромагнитные свойства достаточно большого числа сред. Так, если в
уравнениях (1.6), (1.7)
- проводимость. Они охватывают
электромагнитные свойства достаточно большого числа сред. Так, если в
уравнениях (1.6), (1.7) ![]() ,
, ![]() и
и ![]() -
скаляры, то среда считается однородной, изотропной и линейной (для неоднородных
веществ они зависят от координат).
-
скаляры, то среда считается однородной, изотропной и линейной (для неоднородных
веществ они зависят от координат).
При исследовании электромагнитных колебаний и волн большое значение имеют электромагнитные поля, изменяющиеся во времени по синусоидальному закону, т.е. колеблющиеся с вполне определенной частотой. Такие поля называют монохроматическими или гармоническими. При математическом исследовании монохроматических процессов, подчиняющихся линейным уравнениям, целесообразно ввести комплексные обозначения.
Поскольку сами уравнения
Максвелла (1.2) – (1.5) линейны, то при линейном характере материальных
уравнений (1.6), переход к комплексным обозначениям осуществляется следующим
образом. Векторам напряженности электрического и магнитного полей в данной
точке ![]() и
и ![]() приводятся
в соответствии комплексные векторные амплитуды
приводятся
в соответствии комплексные векторные амплитуды ![]() и
и ![]() . Связь между физическими величинами и
их комплексными амплитудами дается следующими соотношениями:
. Связь между физическими величинами и
их комплексными амплитудами дается следующими соотношениями:
![]() ,
, ![]() , (1.15)
, (1.15)
где Re – вещественная часть
комплексного вектора, стоящего в фигурной скобке; ![]() -
круговая частота исследуемого монохроматического процесса, связанная с обычной
частотой f и периодом колебаний T формулой
-
круговая частота исследуемого монохроматического процесса, связанная с обычной
частотой f и периодом колебаний T формулой
![]() .
(1.16)
.
(1.16)
Аналогичным образом вводятся комплексные амплитуды для всех
физических величин, входящих в уравнения электродинамики и колеблющихся с
частотой ![]() .
.
Подставляя выражения (1.15) в уравнения Максвелла (1.2) и (1.4) и пользуясь формулами дифференцирования и материальными соотношениями (1.6), получаем уравнения для комплексных амплитуд:
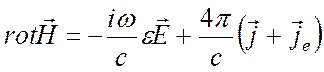 , (1.16)
, (1.16)
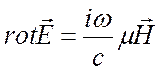 .
(1.17)
.
(1.17)
Заметим, что в случае немонохроматических процессов для исследования электромагнитных волн с произвольной зависимостью от времени можно использовать спектральное разложение, например, разложение поля в интеграл Фурье:
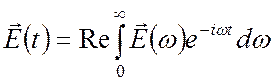 ,
, 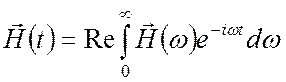 , (1.18)
, (1.18)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.