9.
Квазистационарные явления. Квазистационарные явления в электродинамике. Потенциалы,
описывающие квазистационарные поля. Теория цепей.. ![]() - теорема
теории размерности. Диффузия электрического поля. Отсутствие эффекта
запаздывания в квазистационарных полях. Скин-эффект Униполярная индукция.
Движение проводника в магнитном поле. Закон Ома для движущегося проводника.
Возбуждение тока ускорением Электромагнитные волны в линиях передачи.
Телеграфные уравнения. Гармонический процесс в длинной линии.
- теорема
теории размерности. Диффузия электрического поля. Отсутствие эффекта
запаздывания в квазистационарных полях. Скин-эффект Униполярная индукция.
Движение проводника в магнитном поле. Закон Ома для движущегося проводника.
Возбуждение тока ускорением Электромагнитные волны в линиях передачи.
Телеграфные уравнения. Гармонический процесс в длинной линии.
9.1.
Квазистационарные явления в электродинамике. Потенциалы, описывающие
квазистационарные поля. Задачи
электродинамики в сплошных материальных средах описываются замкнутой системой
уравнений: уравнениями Максвелла совместно с уравнениями материальных связей.
Система уравнений Максвелла это линейная система дифференциальных уравнений
(имеется в виду описание непрерывных полей) в частных производных. Возможно
использование этой системы в различных формах, например, для неизвестных
функций ![]() :
:
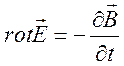 , (9.1)
, (9.1)
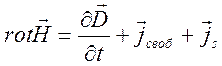 , (9.2)
, (9.2)
![]() , (9.3)
, (9.3)
![]() , (9.4)
, (9.4)
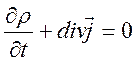 . (9.5)
. (9.5)
Сейчас будем использовать материальные соотношения в простейшем виде. Считаем, что они представляют собой линейные локальные связи (сделано пренебрежение влиянием пространственной и временной дисперсиями)
![]() .
.
В
предыдущих разделах анализировались свойства статических полей, не зависящих от
времени. Учет такой зависимости приводит к значительному усложнению решения
задач электродинамики. Однако, имеется круг проблем, когда допустимо
использовать приближенный учет влияния зависимости полей от времени. Одно из
таких приближений (квазистационарное приближение) основано на
пренебрежении зависимостью вектора индукции ![]() от
времени в уравнении (9.2)
от
времени в уравнении (9.2) 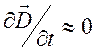 . Это приближение
основано на пренебрежении токами смещения по сравнению с токами проводимости
. Это приближение
основано на пренебрежении токами смещения по сравнению с токами проводимости
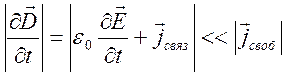 . (9.6)
. (9.6)
Для
гармонического поля ![]() условие (9.6) с учетом
приведенных простейших материальных соотношений запишется в виде ограничения на
частоту сверху
условие (9.6) с учетом
приведенных простейших материальных соотношений запишется в виде ограничения на
частоту сверху
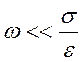 . (9.7)
. (9.7)
В
том случае, если поля не гармонические, то в условии (9.7) следует заменить ![]() на
на ![]() , где
, где ![]() - характерный временной масштаб изменения
полей во времени. Приведем оценку частот, удовлетворяющих условию (9.7) для
почв и для металлов. Для почв
- характерный временной масштаб изменения
полей во времени. Приведем оценку частот, удовлетворяющих условию (9.7) для
почв и для металлов. Для почв ![]() , для меди
, для меди ![]() , относительная диэлектрическая
проницаемость их
, относительная диэлектрическая
проницаемость их ![]() , так что
, так что ![]() .
Условие (9.7) дает ограничения
.
Условие (9.7) дает ограничения
![]() для почв,
для почв,
![]() для меди.
для меди.
Как будет видно из дальнейшего исследования, квазистационарное приближение соответствует пренебрежению эффектом запаздывания при распространении электромагнитных волн в среде.
Ниже
ограничимся случаем ![]() , и будем иметь квазистационарное
описание полей
, и будем иметь квазистационарное
описание полей
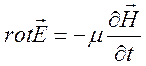 , (9.8)
, (9.8)
![]() , (9.9)
, (9.9)
![]() , (9.10)
, (9.10)
![]() , (9.11)
, (9.11)
Равенство (9.10) позволяет ввести векторный потенциал
![]() . (9.12)
. (9.12)
Из уравнения (9.8) получаем представление для электрического поля
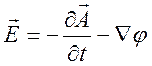 ,
,
где
![]() произвольная функция.
произвольная функция.
Уравнение (9.11) приводится к виду
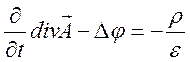 ,
, ![]() . (9.13)
. (9.13)
Потенциал
![]() произвольный, его выберем так, чтобы имело
место уравнение электростатики
произвольный, его выберем так, чтобы имело
место уравнение электростатики
![]()
Согласно (9.13), это порождает калибровку Кулона:
![]() . (9.14)
. (9.14)
Уравнение
(9.9) при учете представления ![]() , принимает вид
, принимает вид
![]() . (9.15)
. (9.15)
Это
соотношение дает связь между двумя неизвестными функциями ![]() и
и ![]() .
.
Рассмотрим
частный случай описания квазистационарного процесса в ситуации: ![]() :
:
![]() ,
,
так как ![]() то при
то при ![]() имеем
имеем ![]() при
при ![]() . Из
уравнения
. Из
уравнения
![]()
следует ![]() , т.е. свободные и сторонние заряды
компенсируют друг друга. Из уравнения непрерывности
, т.е. свободные и сторонние заряды
компенсируют друг друга. Из уравнения непрерывности 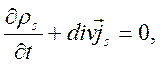 при
при ![]() следует:
следует: ![]() не
зависит от времени. Так как
не
зависит от времени. Так как ![]() , значит и
, значит и ![]() не зависит от времени в такой ситуаци.
не зависит от времени в такой ситуаци.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.