68. Нестационарные потоки событий и потоки с ограниченным последействием. Их математические модели
Теорема Хинчина была обобщена на случай когда слагаемые потоки являются неординарными и нестационарными, при этом если слагаемые потоки независимы и их интенсивность приблизительно одинакова, то суммарный поток близок к Пуассоновскому, но с переменным параметром l(t)
l(t) – мгновенная плотность
Мгновенная плотность является пределом отношения среднего числа событий, приходящих на элементарный интервал к длине этого интервала, когда последний стремится к 0.
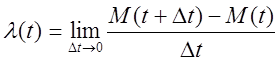
M(t) –математическое ожидание количества
событий на соответствующем интервале. Доказано, что для такого потока число
событий попавших на интервал Z также распределено по Пуассоновскому
закону, но вероятность зависит P(t0,n,z)
=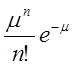 ,
где
,
где 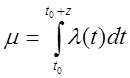
Аналогично тому как была выделена функция плотности распределения длины интервала для простого Пуассоновского потока, то мы могли бы получить аналогичную функцию плотности
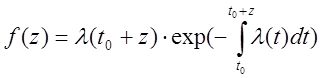
Потоки с ограниченным последействием (потоки Пальма)
Другим обобщением простейшего Пуассоновского потока является потоки Пальма.
Опр. Потоком Пальма называется поток обладающий свойствами ординарности, стационарности и независимости интервала времени Т между событиями. Требование независимости интервала Т является более слабым, чем требование без последействия, поэтому такие потоки называют с ограниченным последействием.
Теорема: Пусть в систему поступает поток требований типа Пальма. Заявка, заставшая все каналы занятыми получает отказ. Поток требований, получивших отказ также является потоком Пальма
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.