54. Двойственность в ЛП (двойственные задачи, теоремы двойственности).
Прямая задача Двойственная
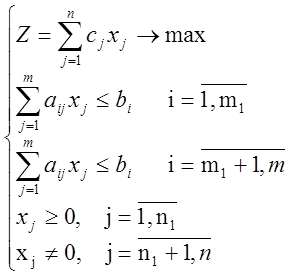
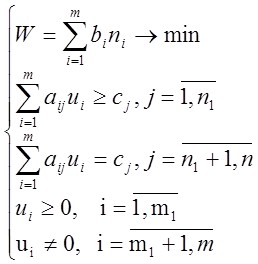
1. Каждому ограничению прямой задачи соответствует переменная двойственной задачи, то есть число переменных двойственной задачи равно числу ограничений первой задачи. Каждой переменной прямой задачи соответствует ограничение двойственной задачи, то есть число ограничений двойственной задачи равно числу переменных прямой задачи
2. Максимизация целевой функции прямой задачи заменяется минимизацией целевой функции двойственной
3. Матрица коэффициентов двойственной задачи получается путем транспонирования матрицы коэффициентов прямой задачи
4. Коэффициенты целевой функции двойственной задачи это есть свободные члены ограничений прямой задачи и наоборот
5. Каждому ограничению типа неравенство прямой задачи соответствует свободная по знаку переменная двойственной задачи
6. Каждой неотрицательной переменной прямой задачи соответствует ограничение типа неравенство двойственной задачи.
Если одна из взаимодвойственных задач имеет оптимальное решение, то и двойственная ей задача имеет оптимальной решение и выполняется равенство Z(x*)=W(u*), где x*, u* - оптимальное решение задач (1) и (2). Если прямая задача не имеет решения, то и двойственная задача не имеет решения.
Следствие: (1-й критерий оптимальности) В этом контексте понятие критерия оптимальности выступает в роли некоторого математического выражения…
Для того, чтобы x’ и u' – допустимые решения задач (1) и (2) были оптимальны необходимо и достаточно чтобы выполнялось условие вида Z(x’)=W(u’)
2 критерий. Для того чтобы x’ и u’ – допустимые решения прямой и двойственной задачи были оптимальными необходимо чтобы выполнялись условия дополняющей нежесткости
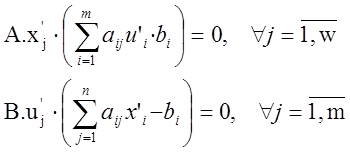
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.