Министерство Образования Российской Федерации
Санкт-Петербургский государственный горный институт (технический университет) им. Г. В. Плеханова
Кафедра высшей математики
Расчетно-графическое задание №1
по дисциплине: высшая математика
Выполнил: студент группы ТО-02 _________ Исиченко А.С. (подпись) (Ф. И. О)
Проверил: профессор __________ Господариков А.П.
(должность) (подпись) (Ф. И. О)
Санкт-Петербург
2004
Задание:
1. Найти коэффициенты ряда Фурье для заданной функции на заданном промежутке.
2. Оставить в получившемся ряде 3 гармоники(n=3)
3. Вычислить среднеквадратическую погрешность
4. Начертить:
- график первой гармоники
- график второй гармоники
- график третьей гармоники
- график приближенной функции и график самой функции.
Исходная функция
![]()
Решение:
![]()
Функция
определена на отрезке ![]() и имеет конечное число
точек разрыва , следовательно, для данной функции выполнены все условия теоремы
Дирихле. Следовательно, данную функцию можно разложить в ряд Фурье.
и имеет конечное число
точек разрыва , следовательно, для данной функции выполнены все условия теоремы
Дирихле. Следовательно, данную функцию можно разложить в ряд Фурье.
Т.к. функция определена на
промежутке ![]() (l-любое
положительное число) и является четной, тогда можно показать, что разложение
функции в ряд Фурье на данном промежутке имеет вид:
(l-любое
положительное число) и является четной, тогда можно показать, что разложение
функции в ряд Фурье на данном промежутке имеет вид:
![]()
где коэффициенты ряда Фурье вычисляются по формулам:
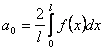
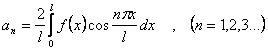
![]()
Применим эти формулы для данной функции
1.
вычисляем ![]()
![]()
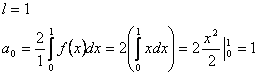
Из построенного графика
видно, что функция обладает свойством четности, поэтому ![]() b
b![]() =0 (n=1,2,3….);
=0 (n=1,2,3….);
2.
вычисляем ![]() , применяя формулу интегрирования по частям
, применяя формулу интегрирования по частям![]()

Таким образом,
![]() ;
;![]() ;
;![]()
следовательно исходная функция разложится в ряд Фурье:
![]()
Для построения приближающей функции представим три гармоники:
1.
![]()
2.
![]()
3.
![]()
Можно предположить, что сумма
этих гармоник будет приближаться к данной функции с погрешностью ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.