=> | K’P’| - кратчайшее расстояние от т.P’ до K’N’
Кратчайшее расстояние от P’ до K’N’
измеряется по перпендикуляру => ![]() => две взаимно перпендикулярных направления
найдены.
=> две взаимно перпендикулярных направления
найдены.
![]()
Доказательство теоремы 3:
Пусть дано АП А плоскости
В качестве начальной СК определяющей данное АП А
возьмем ПДСК ![]() , причем i, j
такие векторы, которые при данном АП→ в 2 взаимно
, причем i, j
такие векторы, которые при данном АП→ в 2 взаимно ![]() вектора. Такие векторы можно найти в силу леммы.
вектора. Такие векторы можно найти в силу леммы.
Пусть система ![]()
![]()
![]()
причем ![]() , но
, но ![]() ,
, ![]() ,
, ![]() (в общем случае)
(в общем случае)
Рассмотрим преобразование сжатия (![]() ) вдоль вектора
) вдоль вектора ![]() .
.
![]() - преобразование, при котором любой вектор
- преобразование, при котором любой вектор ![]() изменяет свою длину в
изменяет свою длину в ![]() раз, соответственно, вектор перпендикулярный этому
направлению не изменяет свою длину.
раз, соответственно, вектор перпендикулярный этому
направлению не изменяет свою длину.
![]()
![]() (единичный)
(единичный)
![]()
![]()
![]()
Рассмотрим АП сжатие ![]() , которое переводит, сжатие вдоль вектора
, которое переводит, сжатие вдоль вектора ![]() с
коэффициентом
с
коэффициентом ![]() .
.
![]()
![]()
![]()
Рассмотрим композицию АП
![]()
![]() (движение по определению) D
(движение по определению) D
– преобразование, в котором ПДСК →ПДСК
![]()
![]() - сжатие вдоль вектора
- сжатие вдоль вектора ![]() с коэффициентом
с коэффициентом ![]()
![]() - сжатие вдоль вектора
- сжатие вдоль вектора ![]() с коэффициентом
с коэффициентом ![]()
А – произведение АП. Ч.т.д.
Теорема 3’. Произвольное АП пространства можно представить в виде композиции некоторого движения пространства и трех сжатий по взаимно перпендикулярны направлениям.
Доказательство: аналогично.
Движения, их свойства и виды.
См. свойства АП, опр., что писали ранее.
Свойства движения:
![]() При движении плоскости произвольный треугольник
переходит в треугольник, равный первоначальному.
При движении плоскости произвольный треугольник
переходит в треугольник, равный первоначальному.
Доказательство: признак равенства треугольника по трем сторонам. (ранее мы доказали утверждение, что при движении расстояния между точками сохраняется)
![]() При движении углы между векторами сохраняются.
При движении углы между векторами сохраняются.
Доказательство:
по свойству ![]() . Приложим 2 вектора общему началу, соединим концы,
получим треугольник, по свойству 1 этот треугольник перейдет при движении в
равный ему треугольник, следовательно, соответствующие углы в этих
треугольниках равны.
. Приложим 2 вектора общему началу, соединим концы,
получим треугольник, по свойству 1 этот треугольник перейдет при движении в
равный ему треугольник, следовательно, соответствующие углы в этих
треугольниках равны.
![]() При движении площади треугольников сохраняются.
Очевидно.
При движении площади треугольников сохраняются.
Очевидно.
![]() При движении любая плоская замкнутая фигура переходит
в фигуру, равную первоначальной.
При движении любая плоская замкнутая фигура переходит
в фигуру, равную первоначальной.
Виды движения:
Аналитическое выражение движения (формулы движения).
Из материала 1 семестра известны формулы связи старых и новых базисных векторов при преобразовании ПДСК.
![]()
Запишем формулы преобразований координат точек плоскости при переходе к новой ПДСК: т. М’(x’; y’) в старой ПДСК и М’(x;y) в новой ПДСК:
![]()
но x; y – координаты т М в старой ПДСК. Поэтому данные формулы выражают связь координат точки после движения с координатами прообраза этой точки до движения в одной и той же старой ПДСК.
Движение: собственное (верхние знаки в середине формул), несобственное (нижние знаки).
Определение
Движение называется собственным, если обе ПДСК, через которые задается это движение, одинаковой ориентации. В противном случае оно несобственное.
DC - собственное движение (верхние знаки)
![]()
Найдем двойную точку собственного движения.
![]()
![]()
![]() – условие двойной точки
– условие двойной точки
![]()
![]()
Решим систему методом Крамера
![]()
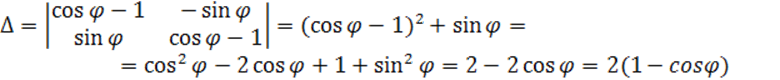
![]()
![]()
![]()
![]()
![]()
Условие, что это решение есть и единственное по теореме
Крамера ![]() . Единственная двойная точка собств. движения с
координатами x0 и y0.
. Единственная двойная точка собств. движения с
координатами x0 и y0.
(*) ![]()
DC ![]() (V)
(V) ![]()
тогда преобразование DC имеет единственную двойную точку.
(*)→ в (V) и получим:
![]() (VV)
(VV)
Рассмотрим геометрический смысл формул (VV).
Рассмотрим вектор ![]() , где
, где ![]() – двойная точка DC
– двойная точка DC
![]()
![]() => из формул (VV)
=> из формул (VV)
![]()
Обозначим
![]()
![]()
![]()
![]()
(**) ![]() - формулы поворота вектора на угол φ
- формулы поворота вектора на угол φ
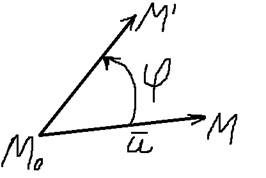
Найдем угол между векторами {α;β} и {α’;β’}
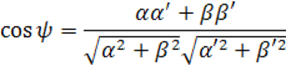
![]()
![]()
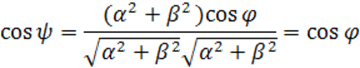
![]()
Мы доказали, что формулы
DC (VV) ![]()
описывают поворот плоскости вокруг неподвижной точки М0
на угол ![]() .
.
Т.о. можно считать, что начальные формулы преобразования DC (V), это тоже формулы поворота плоскости вокруг т. М0 на угол φ.
Частный случай формулы (V) DC
(V) ![]()
1) если a=0, b =0: поворот плоскости вокруг начала координат
DC0: ![]()
![]()
2) ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.