Анализ и синтез механизма стана холодной калибровки труб (Синтез кулачковых механизмов)

6. Синтез кулачковых механизмов.

Синтез кулачковых механизмов заключается в определении основных размеров механизма и профиля кулачка по заданному движению выходного звена.

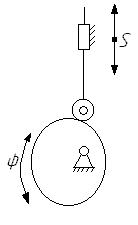
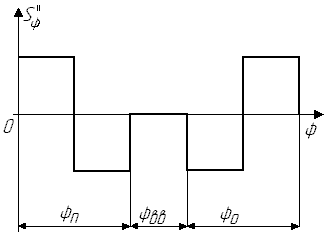
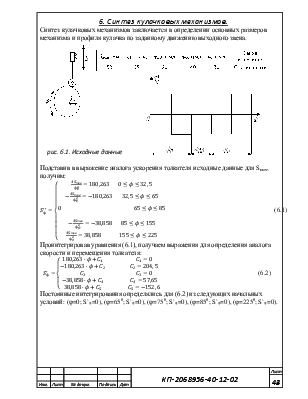
рис. 6.1. Исходные данные

Подставив в выражение аналога ускорения толкателя исходные данные для S_max, получим:

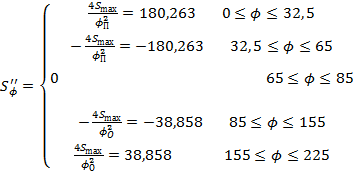                                                                             (6.1)

Проинтегрировав уравнения (6.1), получаем выражения для определения аналога скорости и перемещения толкателя:

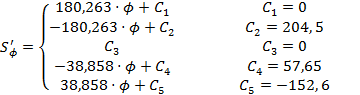                                                 (6.2)

Постоянные интегрирования определялись для (6.2) из следующих начальных условий: (φ=0; S`<sub>φ</sub>=0), (φ=65<sup>0</sup>; S`_φ=0), (φ=75⁰; S`<sub>φ</sub>=0), (φ=85<sup>0</sup>; S`_φ=0), (φ=225⁰; S`_φ=0).

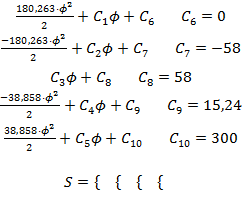                                                       (6.3)

Постоянные интегрирования определялись для (6.2) из следующих начальных условий: (φ=0; S_φ=0), (φ=65⁰; S_φ=58), (φ=75⁰; S_φ=58), (φ=85⁰; S_φ=58), (φ=225⁰; S_φ=0).

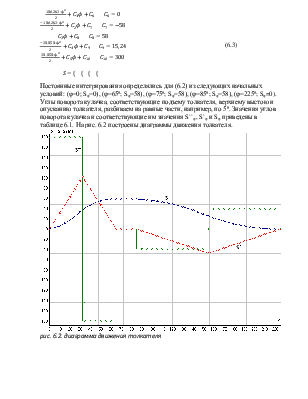
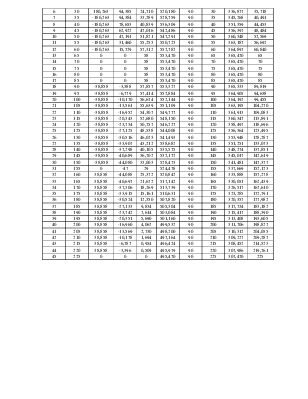
Углы поворота кулачка, соответствующие подъему толкателя, верхнему выстою и опусканию толкателя, разбиваем на равные части, например, по 5⁰. Значения углов поворота кулачка и соответствующие им значения S``_φ, S`_φ и S_φ приведены в таблице 6.1. На рис. 6.2 построены диаграммы движения толкателя.

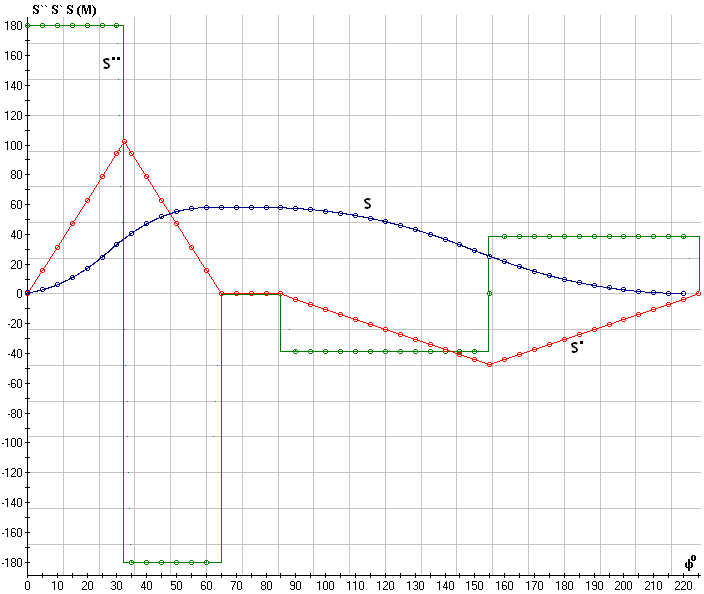
рис. 6.2. диаграмма движения толкателя

Начальный радиус кулачка определяется по формуле:

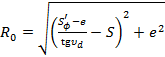                                                                                          (6.4)

В нашем случае смещение e оси движения толкателя относительно центра вращения кулачка равно нулю (см. начальные условия рис. 6.1). И (6.4) примет вид (υ_d на фазе подъема подставлять со знаком плюс, а на фазе опускания – со знаком минус):

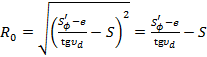                                                                                 (6.5)  (6.5)

Если определить начальный радиус R₀ для всех положений механизма, то наибольшее значение R₀, при котором выполняется условие υ≤υ_d, будет искомым. Чтобы не определять радиус R₀ для нескольких положений механизма, можно найти его экстремальное значение. Для этого в формулу (6.5) подставляем выражения (6.3)

и (6.2).

При прямоугольном законе аналога ускорения R₀ будет наибольшим на участке подъема при φ=φ_П/2=32,5⁰, а на участке опускания при φ=φ_П+φ_ВВ+φ_О/2=155⁰.

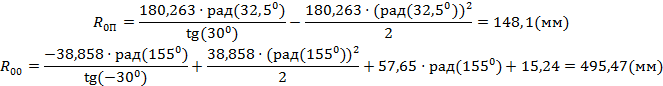
За начальный радиус кулачка принимаем наибольший радиус R₀=495,47(мм).

Центровой профиль кулачка рассчитываем в полярных координатах по формулам

                                                                                   (6.6)

                                                                                                   (6.7)

где R –величина радиус-вектора центрового профиля кулачка; a- полярный угол;

b и b₀ –углы, определяемые из выражений

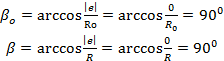                                                                              (6.8)

С учетом того, что в нашем случае е=0 формулы (6.6) и (6.7) примут вид:

                                                                                        (6.6)

                                                                                                                  (6.7)

При φ=20⁰ будем иметь

Для остальных углов поворота кулачка значения полярных координат и углов β

приведены в таблице 6.1.

Для определения профиля кулачка выбираем радиус ролика из условия

 Принимаем радиус ролика r=188(мм).

Величину радиус-вектора и полярный угол профиля кулачка рассчитываем по формулам

                                                                                       (6.8)

                                                                                                         (6.9)

Знак плюс в выражении (6.9) соответствует фазе подъема, а знак минус - фазе опускания.

В формуле (6.8) q - угол между радиус-вектором центрового профиля и радиусом ролика

                                                                                  (6.10)

где                                                                    (6.11)

а с учетом того, что у нас β=90⁰ формула (6.11) примет вид:

                                                                                               (6.12)

В выражении (6.9) Da - угол между радиус-вектором центрового профиля и радиус-вектором профиля кулачка,

                                                                                              (6.13)

Определяем полярные координаты профиля кулачка. При φ=20⁰ имеем:

В остальных положениях механизма результаты расчетов приведены в таблице 6.1.

Для построения центрового профиля и профиля кулачка выбираем масштабный коэффициент длин µ = 6мм/мм. С учетом принятого масштабного коэффициента из точки О – центра вращения кулачка проводим окружность радиусом R₀. От начального радиус-вектора ОА₀ откладываем углы α₁, α₂, и далее