Определение и структура задачи идентификации системы управления, страница 2

y_m=M(u)- выход модели,

       y- выход объекта, то

e называется ошибкой выхода или невязкой (рис. 1.1).

 

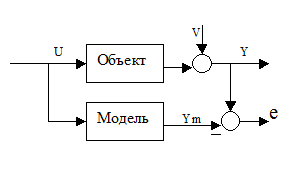
Рис.1.1

Если

, где U_m=M^-1(y) означает вход модели, вызывающей выход y (допускается обратимость модели ), то e называется ошибкой входа(рис.1.2).

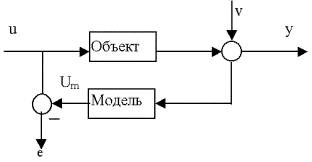
Рис.1.2

В общем случае ошибка определяется формулой

 

и называется обобщенной (рис.1.3).

 

Рис.1.3

В классе линейных объектов при значительном объёме априорной информации удаётся построение оптимальной в известном смысле (квадратичный критерий подобия объекта и модели) настраиваемой модели. Такая модель наилучшем образом предсказывает выходную величину идентифицируемого объекта, а её структура однозначно зависит от точки приложения к объекту помех.

В некоторых случаях точность идентификации и следовательно качество решения задачи можно охарактеризовать отклонением конкретных содержательных характеристик объекта и модели (весовых функций объекта и модели, плотностей распределения вероятностей выходных сигналов, оценок корреляционных функций и т.п.). Все методы данной группы относятся к непараметрическим.  

Вычислительный метод решения задачи - это алгоритм идентификации в значительной мере зависящий от структуры модели и выбранного критерия подобия объекта и модели. Часто критерий качества выбирается квадратичным, в виде среднего значения квадрата невязки. Это связано с возможностью получения линейных уравнений и организации эффективных в вычислительном отношении алгоритмов идентификации.

    Оценка адекватности объекта и полученной модели известна под названием “процедур подтверждения модели” состоит в оценки соответствия построенной модели наблюдаемым данным (анализ и воспроизведение данных), априорной информации и цели идентификации.     

В  зависимости от способа обработки данных и организации вычислительного процесса, методы идентификации можно разделить по типу реализации на ретроспективные (явные) и адаптивные (неявные). Первая группа методов характеризуется использованием явных математических выражений и выполнением серии предварительных вычислений и преобразований: вычисление последовательности значений частотной характеристики, значений оценок корреляционных функций в отдельных точках и т.п. Получение в явной форме окончательного результата происходит однократно, после выполнения конечного числа элементарных операций, как решение некоторой совокупности уравнений. Данный тип реализации требует значительной памяти ЭВМ и не может быть получен как результат некоторых  приближенных вычислений. На рис.1.4 изображена модельная реализация вычисления оценки взаимной корреляционной функции R_Уи(t) по наблюдаемым данным. Оценка используется в основном уравнении идентификации.

 

                                            Рис.1.4

Во втором, адаптивном способе реализации, происходит целенаправленное изменение (подстройка) параметров настраиваемой модели так, чтобы критерий подобия с течением времени стремился к минимуму. Подобная процедура не требует повторной обработки всей совокупности наблюдений и позволяет обрабатывать поступающие данные последовательно в процессе их поступления, в режиме нормального функционирования. Последнее обстоятельство особенно важно при построении адаптивных систем управления, использующих на каждом шаге алгоритма адаптации результаты текущей идентификации (рис.1.5)

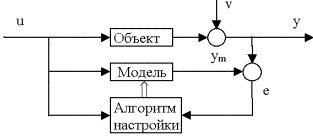
Рис.1.5

Последний тип реализации обеспечивает полную обработку измерений на каждом шаге до начала следующего шага, и возможность использовать промежуточные результаты в решении многих прикладных задач. Методы данной группы называют рекуррентными методами идентификации.

Обобщаемая функциональная схема задачи идентификации изображена на рис.1.6

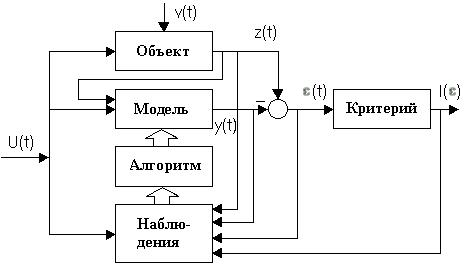
Рис.1.6

Итеративная схема решения задачи идентификации (выбор типа модели, реализация алгоритма, оценка адекватности, повторный выбор типа модели…) фактически представляет собой реализацию традиционной инженерной концепции “проб и ошибок”.

Здесь u(t)- входная последовательность;

          z(t) – выход объекта;

         y(t) – выход модели;

         v(t)- сигнал помехи;

         e(t)- сигнал невязки.