Алгоритмы сжатия данных. Методы ориентированные на конкретную структуру или содержимое данных. Статистические методы

Если же эту строку преобразовать в число, то для ее хранения в памяти достаточно 4 байта. Тоже можно сделать для телефона. Дату можно хранить в упакованном виде. День – 5 бит, месяц – 4 бита, год – 7 бит. Итого 2 байта.

Алгоритмы сжатия данных первого класса

Кодирование элементов, имеющих одинаковое значение Обычно в населенном пункте встречается много однофамильцев, а число различных фамилий и имен ограничено. Наиболее распространенные 256 имен можно закодировать одним байтом, а имена не попавшие в этот перечень, представить полностью. Таким же способом можно закодировать названия улиц. Учитывая, что фамилии часто образованы от имен, ту часть фамилии, которая совпадает с именем, можно заменить кодом имени. Этот способ сжатия данных требует наличия кодовой таблицы как при кодировании, так и при декодировании.

Алгоритмы сжатия данных первого класса

Сжатие упорядоченных имен Поскольку телефонный справочник лексикографически упорядочивается по фамилиям, то начальные символы фамилий в соседних элементах часто совпадают. Тогда в последующих элементах справочника вместо начальных символов фамилий в первом байте можно указать число совпадающих символов. Пример. Исходное представление Сжатое представление Иванов Иванов Иванов 6 Ивановский 6ский Иванченко 4ченко Ивашкин 3шкин Ивашов 4ов (или 3шов) Ивлиев 2лиев

Алгоритмы сжатия данных второго класса

Групповое кодирование Сжатие происходит за счет того, что в исходных данных встречаются цепочки одинаковых байтов. Заменяя их на пары < счетчик, значение > уменьшают избыточность данных. Дополнительной памяти алгоритм не требует, выполняется быстро за один проход. При передаче данных этот способ применяется и для сжатия цепочки одинаковых битов.

Кодирование

Пусть заданы алфавиты А={a1,a2,…,an}, B={b1,b2,…,bm} и функция F: S->B*, где S – некоторое множество слов в алфавите A. Тогда функция F называется кодированием, элементы множества S – сообщениями, а элементы β=F(α) – кодами. Обратная функция к функции F называется декодированием. Кодирование может сопоставлять код всему сообщению как единому целому или строить код сообщения из кодов его частей (например, букв).

Алфавитное кодирование

Последовательность букв называется словом. Количество букв в слове называется длиной слова. Если α=α1α2, то α1 называется началом или префиксом, а α2 – окончанием или постфиксом слова α. Алфавитное кодирование задается схемой (или таблицей кодов). Схема называется разделимой, если любое слово составленное из элементарных кодов, единственным образом разлагается на элементарные коды. Алфавитное кодирование с разделяемой схемой допускает декодирование. Схема называется префиксной, если элементарный код одной буквы не является префиксом элементарного кода другой буквы.

Алфавитное кодирование

Теорема. Префиксная схема является разделимой. Свойство быть префиксной является достаточным, но не является необходимым для разделимости схемы. Чтобы схема алфавитного кодирования была разделимой необходимо, чтобы длины элементарных кодов удовлетворяли соотношению, известному как неравенство Макмиллана: ∑ 1/(2↑li) < 1, где li – длина i-го элементарного кода.

Алфавитное кодирование с минимальной избыточностью

Пусть заданы алфавит А={a1,…,an} и вероятности появления букв в сообщении P={p1,…,pn}. Для каждой схемы алфавитного кодирования математическое ожидание коэффициента увеличения длины сообщения при кодировании определяется следующим образом: ∑ pi*li и называется средней ценой (или длинной) кодирования при распределении вероятностей P. Алфавитное кодирование, для которого цена минимальна, называется кодированием с минимальной избыточностью или оптимальным.

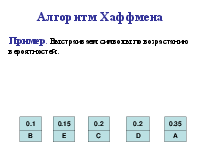
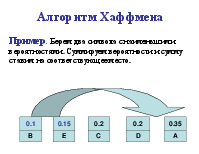
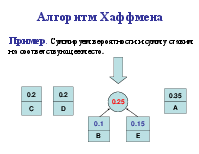
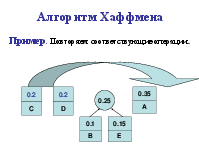
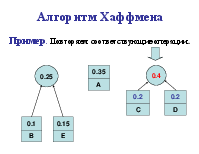
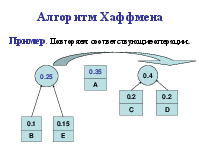
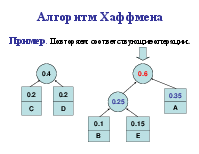
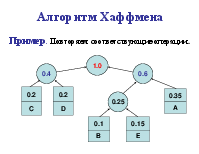
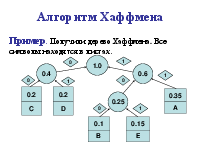
Алгоритм Хаффмена

Алгоритм использует частоту (вероятность) появления элементов (символов) в данных. Элементы входного потока, которые встречаются чаще (имеют большую вероятность), кодируются цепочкой битов меньшей длины, в встречающиеся редко – цепочкой большей длины. Алгоритм выполняется за два прохода: сбор статистики и непосредственное кодирование. Алгоритм требует наличия кодовой таблицы. Таблицы могут быть постоянными или создаваться по результатам сбора статистики при первом проходе.

Алгоритм Хаффмена

Коды Хаффмена обладают двумя важными свойствами. Во-первых, коды Хаффмена являются двоичными кодами с минимальной средней длиной. Во-вторых, кода Хаффмена обладают префиксным свойством. Это означает, что ни один код в полученном множестве кодов не имеет