Фундаментальные структуры данных. АВЛ-деревья. Метод «преобразуй и властвуй»

Фундаментальные структуры данных

АВЛ-деревья

Метод «преобразуй и властвуй»

• Рассмотрим группу методов, основанных на идее преобразования («преобразуй и властвуй»). Такие методы работают в две стадии. Сначала, на стадии «преобразования», экземпляр задачи преобразуется в другой, по той или иной причине легче поддающийся решению, после чего на стадии «властвования» решается полученный в результате преобразования экземпляр задачи. Имеется три основных варианта этого метода:
• Упрощение экземпляра.
• Изменение представления экземпляра.
• Приведение задачи.

АВЛ-деревья

АВЛ-деревья были открыты в 1962 г. двумя советскими математиками – Г.М. Адельсоном-Вельским и Е.М. Ландисом. АВЛ-деревом (AVL-TREE) называется такое бинарное дерево поиска, у которого высота поддеревьев для каждого узла различается не более чем на 1. Максимальная высота АВЛ-дерева с n узлами не превосходит 1,4405*log2(n+1)-0,3277, т.е. затраты на поиск не превосходят 1,45*O(log2n). АВЛ-дерево относится к классу сбалансированных деревьев. При включении и удалении узлов необходимо поддерживать сбалансированность дерева в целом.

АВЛ-деревья

В каждый узел дерева добавляется одно вспомогательное поле, содержащее информацию о равновесности поддеревьев (показатель сбалансированности узла h). Его значение равно разности высот левого и правого поддеревьев. Если вставка нового узла делает АВЛ-дерево несбалансированным, оно преобразуется при помощи поворота. Поворот в АВЛ-дереве представляет собой локальное преобразование поддерева, корень которого имеет показатель сбалансированности, равный +2 или -2; если таких узлов несколько, мы поворачиваем дерево с несбалансированным корнем, который наиболее близок к вновь вставленному листу.

АВЛ-деревья

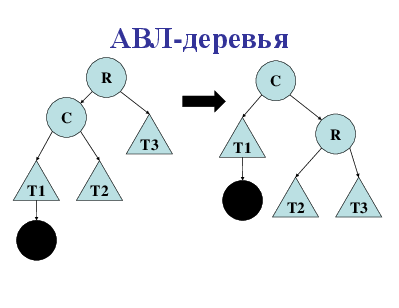
Всего имеется только четыре типа поворотов, причем два из них представляют собой зеркальное отражение двух других. Одиночный правый поворот или R-поворот. Он выполняется после вставки нового ключа в левое поддерево левого дочернего узла корня, который перед вставкой имел показатель сбалансированности +1. Одиночный левый поворот или L-поворот. Он выполняется после вставки нового ключа в правое поддерево правого дочернего узла корня, который перед вставкой имел показатель сбалансированности -1.

АВЛ-деревья

R

C

C

T3

R

T1

T1

T2

T2

T3

АВЛ-деревья

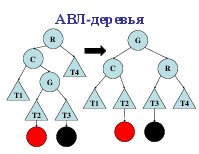
Двойной лево-правый поворот или LR-поворот. Он представляет собой объединение двух поворотов: выполняется L-поворот левого поддерева корня r, за которым следует R-поворот нового поддерева, корнем которого является r. Он выполняется после вставки нового ключа в правое поддерево левого дочернего узла дерева, корень который перед вставкой имел показатель сбалансированности +1.

АВЛ-деревья

R

G

C

T4

C

R

G

T1

T1

T2

T4

T3

T2

T3

АВЛ-деревья

Двойной право-левый поворот или RL-поворот. Он представляет собой зеркальное отражение двойного LR-поворота. Он представляет собой объединение двух поворотов: выполняется R-поворот правого поддерева корня r, за которым следует L-поворот нового поддерева, корнем которого является r. Он выполняется после вставки нового ключа в левое поддерево правого дочернего узла корня, который перед вставкой имел показатель сбалансированности -1.

АВЛ-деревья

В каждый узел дерева добавляется одно вспомогательное поле, содержащее информацию о равновесности поддеревьев (показатель сбалансированности узла h). Его значение равно разности высот левого и правого поддеревьев. struct node { int DATA; int bal; struct node *LPTR,*RPTR; }; int h = 0;

/*Вставка узла в AVL-дерево*/ int insertAVL(int key, struct node **t, int *h) { struct node *t1,*t2,*T; int ret = 0; T = *t; if ( T == NULL) // Если дерево пустое { T=(struct node*) malloc(sizeof(struct node)); T->DATA = key; T->bal = 0; *h=1; T->LPTR = T->RPTR = NULL; }

else // Если дерево не пустое if (key < T->DATA) { insertAVL(key, &(T->LPTR), h); // В левое поддерево if (*h != 0) { switch (T->bal) { case 1: T->bal = 0; *h = 0; break; case 0: T->bal = -1; break; case -1: // балансировка { t1 = T->LPTR; if (t1->bal == -1) // L-поворот { T->LPTR = t1->RPTR; t1->RPTR = T; T->bal = 0; T = t1; }

else // LR-поворот { t2 = t1->RPTR; t1->RPTR = t2->LPTR; t2->LPTR = t1; T->LPTR = t2->RPTR; t2->RPTR = T; if (t2->bal == -1) T->bal = 1; else T->bal = 0; if (t2->bal == 1) t1->bal = -1; else t1->bal = 0; T = t2; } T->bal = 0; *h = 0; } } } }

else if (key > T->DATA) // В правое поддерево { insertAVL(key, &(T->RPTR), h); if (*h == 1) switch (T->bal) { case -1: T->bal = 0; *h = 0; break; case 0: T->bal = 1; break; case 1: // балансировка { t1=T->RPTR; if (t1->bal == 1) // R-поворот { T->RPTR = t1->LPTR; t1->LPTR = T; T->bal = 0; T = t1; }

else // RL-поворот { t2 = t1->LPTR; t1->LPTR = t2->RPTR; t2->RPTR = t1; T->RPTR = t2->LPTR; t2->LPTR = T; if (t2->bal == 1) T->bal = -1; else T->bal = 0; if (t2->bal == -1) t1->bal = 1; else t1->bal = 0; T = t2; } T->bal = 0; *h = 0; } } }

else { gotoxy(1,3); setcolor(RED); outtextxy(10,40,"The key is already in the Tree"); ret=-1; getch(); } *t = T; return ret; }

АВЛ-деревья

Итак, операции поиска и вставки в худшем случае выполняются за время Θ(log2n). Получить точную формулу для средней высоты AVL-дерева, построенного для случайного набора ключей, достаточно сложно, но из многочисленных экспериментом известно, что средняя высота AVL-дерева составляет примерно 1.011*log2n+0.1, за исключением малых значений n. Таким образом, поиск в AVL-дереве требует в среднем того же количества сравнений, что и поиск в отсортированном массиве при бинарном поиске.