Операционная имитация лестничных LC-фильтров

Лекция 22

5.5. Операционная имитация лестничных LC-фильтров

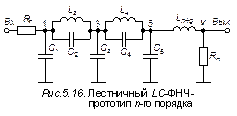                В отличие от методов элементной имитации применение любого из методов операционной имитации приводит к структуре, состоящей из развязанных активных RC-звеньев. Рассмотрим процедуру синтеза структурной схемы активного RC-ФНЧ-прототипа методом матричных преобразований.

В качестве исходной берется схема лестничного LC-ФНЧ-прототипа (схема A) и преобразуется к такому виду, чтобы ее можно было описать одной и той же матрицей как для случая четного, так и нечетного n. Для этого достаточно поменять местами вход и выход и изменить нумерацию элементов, как это показано на рис. 5.16, где   при n четном,  при n нечетном;  в случае нечетного n. Схема в таком виде описывается следующей матрицей проводимостей:

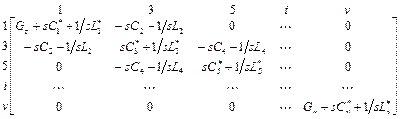, где .

С учетом того, что номера строк и столбцов этой матрицы нечетные, добавляются четные строки и столбцы с ненулевыми элементами

, в результате чего матрица приобретает вид

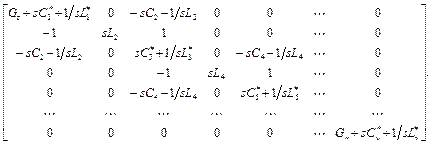
В дальнейшем четные строки , умноженные на , прибавляются к соседним строкам, т.е.

, после чего матрица приводится к виду

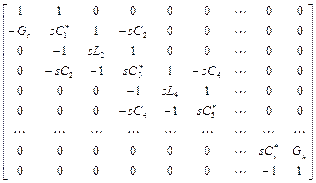.                                  (5.10)

Поскольку  – величины безразмерные, элементы матрицы, расположенные на главной диагонали, фактически являются знаменателями, а остальные элементы – числителями функций передачи развязанных активных звеньев ФНЧ-прототипа.

Чтобы в дальнейшем упростить реализацию звеньев, из матрицы (5.10) исключаются все элементы, содержащие оператор s и расположенные вне главной диагонали. Для этого в цикле по  к i-м строкам и столбцам прибавляются ()-е строки и столбцы, умноженные на коэффициенты :

, в результате чего получается матрица

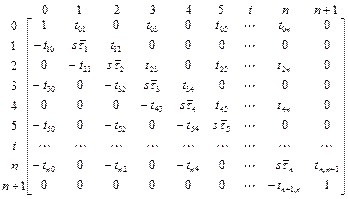,                               (5.11)

которая отличается тем, что у нее все нечетные (j-е) наддиагонали (и поддиагонали) содержат ненулевые элементы, расположенные на пересечении j-х наддиагоналей (при ) и четных строк (j-х поддиагоналей и четных столбцов). Матрица функций передачи фильтра четного порядка отличается от (5.11) тем, что у нее все элементы n-й строки и n-го столбца, за исключением элементов первой над- и поддиагонали, а также, естественно, элемента главной диагонали, равны нулю. В случае полиномиального фильтра произвольного порядка нулевыми будут все элементы j-х над- и поддиагоналей при .

Для реализации нулей передачи, а также для обеспечения условий низкой параметрической чувствительности достаточно, чтобы на каждой нечетной j-й () над- и поддиагонали находилось только по одному ненулевому элементу, например в 0-й строке и 0-м столбце. Чтобы привести матрицу (5.11) к такому виду, необходимо выполнить следующие операции:

где ; .

Если теперь переместить (используя соответствующие операции со строками и столбцами) ненулевые элементы из 0-й строки и 0-го столбца (кроме ) соответственно в 1-ю строку и 1-й столбец, то можно исключить 0-ю строку и ()-е строку и столбец, что приведет к такому виду матрицы (при четном n):

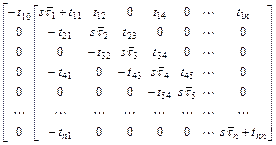,                                         (5.12)

где элементы, обеспечивающие нули передачи, находятся на пересечении первого столбца и четных i-х строк () и имеют отрицательные значения. Расположенные симметрично им (относительно главной диагонали) ненулевые элементы способствуют обеспечению низкой параметрической чувствительности фильтра в полосе пропускания. В матрице фильтра нечетного порядка с полным набором нулей передачи ненулевыми элементами, кроме оговоренных выше, являются также .

Чтобы иметь низкую параметрическую чувствительность не только в полосе пропускания, но и в полосе режекции, матрица (5.12) должна быть симметричной относительно второй диагонали:

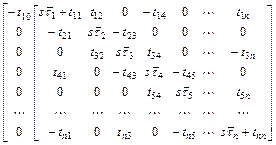,                                        (5.13)

что может быть получено, если на каждом шаге преобразования матрицы (5.11) обеспечивать условия симметрии

, где .

Чтобы в дальнейшем исключить динамические перегрузки на выходах звеньев фильтра, т.е. обеспечить , необходимо в матрице каждую i-ю строку и каждый i-й столбец () умножить на коэффициент , который имеет тот же смысл, что и  в предыдущем подразделе. Иногда удается несколько упростить реализацию звеньев за счет