Аналогичные результаты были бы получены, если бы вместо вала с двумя дисками мы рассмотрели вал с тремя дисками т.д. Следует отметить вероятностный характер явления, так как для того, чтобы оно имело место, начального эксцентриситета вовсе не обязательно.
Если h1=h2=0. Тогда y1=y2=0.
Однако достаточно, чтобы под влиянием случайных причин вал получил сколь угодно малый прогиб, и уравнение вступает в силу.
1.3. Самоцентрирование валов
Вернемся к формуле (1.1) и определим значение, например, у1, когда wраб ®¥.
Разделим все элементы числителя и знаменателя у1 на w2раб. Получим, подставляя вместо A1 и A2 их значения:
у1 = 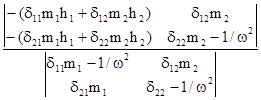
При w2®¥ после раскрытия определителя прогиб вала равен у1= ![]() (1.3)
(1.3)
То есть при w®¥ точки оси вала под нагрузками располагаются по оси вращения. Вал самоцентрируется. Подобное самоцентрирование валов крайне важно, так как при этом эксцентриситет, а с ним и центробежные силы значительно уменьшаются, вал работает спокойно, прогибы стремятся к нулю. Речь идет о конечной скорости, превышающей критическую. Поэтому, когда речь идет о быстровращающихся валах, если вращаются большие массы, целесообразно работать на скоростях вращения выше критической.
При этом гибким называют вал, скорость вращения которого превышает критическую скорость вращения. Жестким называют вал скорость вращения которого ниже критической.
В тех же случаях, когда появление значительных прогибов при переходе через резонанс может вызвать задевание вращающихся деталей о другие детали (неподвижные или сидящие на других валах) целесообразно установить жесткие валы.
Условие виброустойчивости ротора.
Жесткий вал wраб£ 0,7 wкр 1
Гибкий вал 1,3 wкр 1 < wраб <0,7 wкр 2
1.4. Методы расчета критической скорости
1.4.1. Метод наложения
Решение определителя сложно, когда много нагрузок и когда вал переменного сечения. В 1894г. Донкерли вывел формулу:
wкр=![]() , (1.4)
, (1.4)
где wкр - наименьшая возможная критическая частота вращения, 1/с; mi-масса i - го участка вала, кг.
Преобразуя уравнение (1.4) получим:
Sdii mi=SdiiGi/g=1/wкр2=Sfстi /g, где Gi - вес i- го участка вала, Н; g - ускорение свободного падения, м/с2; fст i - статический прогиб вала под грузом (весом вала), м.
Следовательно,
1/wкр2 = 1/wкр 12 + 1/wкр 22 +1/wкр 32 + ×××+1/wкр i2 (1.5)
В случае распределенной по какому-либо закону непрерывной нагрузки q(x), рассмотрим бесконечное число элементарных нагрузок q(x)dx, сосредоточенных в точке с абсциссой х. В этом случае
wкр2=g /![]() q(x) dx, где dхх - прогиб в точке х под действием единичной силы, приложенной в этой
точке; l - длина вала, к которому приложена распределенная нагрузка, м.
q(x) dx, где dхх - прогиб в точке х под действием единичной силы, приложенной в этой
точке; l - длина вала, к которому приложена распределенная нагрузка, м.
В общем случае действия сосредоточенных и распределенных нагрузок
wкр2=1/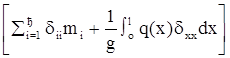
![]() (1.6)
(1.6)
1.4.2. Энергетический метод Рейлея
Применим к колеблющейся балке принцип сохранения энергии (рис. 1.7).
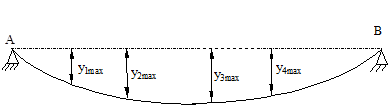
Предполагая колебания без потерь энергии, имеем:
T+V=const; y=0; Т=Тmax, V=0; y=ymax, V=Vmax, Т=0
где V- потенциальная энергия; T- кинетическая энергия.
V= ![]() (1.7)
(1.7)
T= ![]() , (1.8)
, (1.8)
где yi- перемещение центра тяжести отрезка вала, м; yi¢ -первая производная от перемещения по времени, м/с; g -ускорение свободного падения, м/с2; Qi-вес i - го участка вала, Н.
Из закона сохранения энергии следует:
Tmax+0=const; Vmax+0=const; Tmax=Vmax.
Рассмотрим случай колебания с наименьшей частотой, когда все массы одновременно достигают максимального удаления от положения покоя и одновременно через него проходят. Так как грузы совершают гармоническое колебание:
yi=licos(wt+a); (1.9)
yi¢=liwsin(wt+a); (1.10)
yimax=li;
yi¢max=liw, где li-аплитуда колебания i - й точки; t – время, с; a - сдвиг фазы.
Следовательно:
Vmax=![]() (1.11)
(1.11)
Tmax=![]() . (1.12)
. (1.12)
w = wкр=![]()
![]() .
.
Рейлей предположил и доказал, что можно заменить li статическими прогибами балки, т.е. принять:
wкр=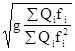 . (1.13)
. (1.13)
где fi- статический прогиб балки под грузом Qi.
fi=di1Q1+di2Q2+.........=
![]() diкQк.
diкQк.
Если желательно учесть массу вала, последний разбивается на ряд участков, в центрах тяжести которых прикладывают сосредоточенные силы, равные их весу.
Коэффициенты влияния для валов с сосредоточенными массами приведены в таблице 1.1
1.5 Влияние на угловую критическую скорость вала различных факторов
1.5.1. Влияние гироскопического момента
Если диск посажен на вал не в середине пролета (рис. 1.8), то при изгибе вала диск поворачивается на определенный угол g, в этом случае на вал действуют центробежная сила Fц и гироскопический момент Мг (рис. 1.8, а, б). Из рис. 1.8, б видно, что Мг препятствует прогибу вала при его прямой синхронной прецессии.
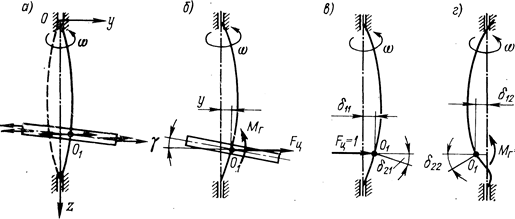
а - схема действия сил на вращающийся диск при изгибе вала; б - схема действия нагрузок на вал со стороны диска при прямой синхронной прецессии; в и г - радиальные и угловые деформации вала от единичных нагрузок
Рис. 1.8. К учету влияния создаваемого диском гироскопического момента на критическую скорость вала
Прогиб y и угол поворота g сечения вала связаны с нагрузками Fц и Мг следующими зависимостями (рис. 1.8, б, г):
![]() (1.14)
(1.14)
Учитывая, что Fц=mw2y; Мг=w2(Jz-Jx)g, где осевой Jzи экваториальный
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.