





этом в уравнение должны входить только искомая продольная сила и груз Р = 1;
3) если используется уравнение моментов, то координату z груза отсчитывают от моментной точки;
4) передаточная (соединительная) прямая находится между узлами рассеченного стержня грузового пояса, левая прямая – слева от передаточной, правая – справа.
Линии влияния усилий в междуопорной части фермы
Построим вначале линии влияния опорных реакций V1 и V5, так как они понадобятся для построения л. в. усилий в междуопорной части фермы. Пользуясь графическим методом, как и для балок, откладываем ординату (+1) под рассматриваемой опорой, под второй опорой нуль, соединяем прямой линией. Линии влияния V1 и V5 показаны на рисунке 3, в, г, они не имеют изломов на протяжении всей фермы.
Линия влияния N3-4’, N3-4, N3’-4’. Проводим сечение I-I через три стержня: 3-4, 3-4’ и 3’-4’, рассматриваем равновесие правой части фермы, если груз Р = 1 левее сечения, и левой части, если груз правее (рисунок 3, б). Расчеты записываем в таблицу 1.
Таблица 1. Построение л. в. N3-4’, N3-4, N3’-4’.
|
Груз Р = 1 слева от сечения I-I (левее узла 3) |
Груз Р = 1 справа от сечения I-I (правее узла 4) |
|
Линия влияния N3-4’(раскос) |
|
|
ΣYправ. ч. = 0, N3-4’ · sin 45º + V5 = 0, N3-4’
= |
ΣYлев. ч. = 0, –N3-4’ · sin 45º + V1 = 0, N3-4’
= |
|
Л. в. N3-4’
= – |
Л. в. N3-4’
= |
|
Линия влияния N3-4 (верхний пояс) |
|
|
ΣМ4’ прав. ч. = 0, N3-4 · а + V5 · а = 0, N3-4 = – V5. |
ΣМ4’ лев. ч. = 0, –N3-4 · а – V1 · 3а = 0, N3-4 = – 3V1. |
|
Л. в. N3-4 = – л. в. V5. |
Л. в. N3-4 = –3 · л. в. V1. |
|
Линия влияния N3’-4’ (нижний пояс) |
|
|
ΣМ3 прав. ч. = 0, –N3’-4’ · а + V5 · 2а = 0, N3’-4’ = 2V5. |
ΣМ3 лев. ч. = 0, N3’-4’ · а – V1 · 2а = 0, N3’-4’ = 2V1. |
|
Л. в. N3’-4’ = 2 · л. в. V5. |
Л. в. N3’-4’ = 2 · л. в. V1. |
По данным таблицы 1 строим линии влияния (рисунок 3, д-ж). Полученные ординаты под узлами 3 и 4 соединяем передаточными прямыми.
Проверяем построения. Для раскосов передаточная прямая должна «пересекать» раскос, для поясов левая и правая прямые должны пересекаться под моментной точкой. В наших линиях влияния эти правила соблюдаются.
Линия влияния N2-2’. Проводим сечение II-II через три стержня: 1-2, 2-3 и 2-2’, рассматриваем равновесие вырезанного узла фермы (рисунок 3, з). Расчеты записываем в таблицу 2.
Таблица 2. Построение л. в. N2-2’.
|
Груз Р = 1 в узле 2 |
Груз Р = 1 вне узла 2 (левее узла 1, правее узла 3) |
|
ΣYузла = 0, – N2-2’ – Р = 0, N2-2’ = – Р = – 1. |
ΣYузла = 0, – N2-2’ = 0. |
По данным таблицы 2 строим линию влияния N2-2’ (рисунок 3, и). Так как сечение II-II пересекает два стержня грузового пояса, будет две передаточные прямые.
Линии влияния усилий в консольной части фермы
Линия влияния N5-6, N5-6’. Проводим сечение III-III через три стержня: 5-6, 5-6’ и 5’-6’ (рисунок 4, а). Для обеих линий влияния будем использовать уравнения моментов, положение груза Р = 1 будем отсчитывать от соответствующей моментной точки, всегда рассматривая равновесие отсеченной консоли.
Для определения N5-6 в качестве моментной точки выбираем узел 6’, где пересекаются стержни 5-6’ и 5’-6’. Здесь помещаем начало системы координат z1, y1 (рисунок 4, б). Для вычисления N5-6’ начало системы координат z2, y2 располагаем в узле 7, причем ось z2 направляем влево (рисунок 4, г). Расчеты записываем в таблицу 3.
Таблица 3. Построение л. в. N5-6 и N5-6’
|
Груз Р = 1 слева от сечения III-III (левее узла 5) |
Груз Р = 1 справа от сечения III-III (правее узла 6) |
|
Линия влияния N5-6 (верхний пояс консоли) |
|
|
ΣМ6’ прав. ч. = 0, – N5-6 · а/2 = 0, N5-6 = 0. |
ΣМ6’ прав. ч. = 0, – N5-6 · а/2 + Р · z1 = 0, N5-6 = Р · 2z1/a = 2z1/a.
|
|
Линия влияния N5-6’ (раскос консоли) |
|
|
ΣМ7 прав. ч. = 0, – N5-6’ · b = 0, N5-6’ = 0. |
ΣМ7 прав. ч. = 0, – N5-6’ · b + Р · z2 = 0, N5-6’ = Р · z2/b = z2/b = z2/0,894а.
|
Здесь b = 2а · sin 26,6º = 0,894a.
По данным таблицы 3 строим линии влияния (рисунок 4, в, д). Полученные ординаты под узлами 5 и 6 соединяем перед аточными прямыми.
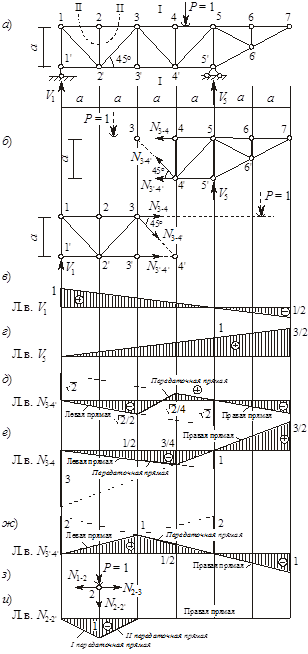
Рисунок 3
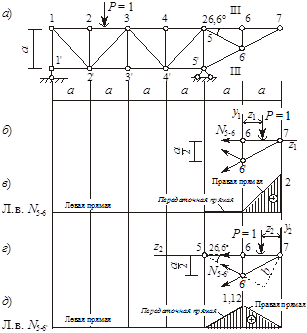
Рисунок 4
4 Определение усилий по линиям влияния
Загрузим линию влияния N3-4’ постоянной нагрузкой q (рисунок 5, а). Подсчитаем площади положительного (ω1) и отрицательных (ω2, ω3) участков (рисунок 5, г):
ω1
= ![]() =
= ![]() ;
ω2 =
;
ω2 = ![]() =
= ![]() ; ω3 =
; ω3 = ![]() =
= ![]() .
.
Определим усилие в стержне 3-4’:
N3-4’ = q(ω1 + ω2 + ω3) = ![]() = –1,414qa.
= –1,414qa.
5 Определение усилий аналитически
Вычислим аналитически усилие в том же стержне. Загрузим ферму узловой нагрузкой (рисунок 5, б) и определим опорную реакцию V1 из уравнения моментов относительно точки 5:
∑М5 = 0; –V14a + 0,5qa 4a + qa 3a + qa 2a + qa · a – qa · a – 0,5qa 2a = 0;
–V14a + 6qa2 = 0; V1 = 6qa2/4a = 1,5qa.
Проведем сечение I-I, отбросим правую часть фермы и рассмотрим равновесие левой. Для нахождения силы N3-4’ составим уравнение проекций на вертикальную ось:
∑Y = 0; V1 – 0,5qa – qa – qa – N3-4’ sin 45º = 0;
1,5qa – 2,5qa – N3-4’ ![]() = 0; N3-4’
=
= 0; N3-4’
= ![]() = –1,414qa.
= –1,414qa.
Результат совпадает с полученным ранее.
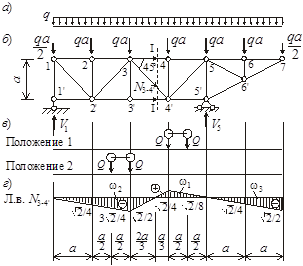
Рисунок 5
6 Вычисление расчетных усилий
Загрузим линию влияния усилия в стержне 3-4’ временной нагрузкой в виде перемещающейся по грузовому поясу крановой тележки весом Р = 3qa.
Давление колес на ось двухосной тележки
Q = Р/4 = 3qa/4 = ¾ qa.
Примем расстояние между осями тележки равным а/2. Поместим тележку на ферму так, чтобы временная нагрузка занимала невыгоднейшее положение (рисунок 5, в). При этом рассмотрим два ее положения – над положительным и отрицательным участками линии влияния.
Вычислим усилие в стержне 3–4’ от временной нагрузки, умножая значения временных сосредоточенных сил Q на ординаты под этими силами.
Положение 1. ![]() .
.
Положение 2. ![]() .
.
Вычислим суммарные усилие в стержне 3–4’ от постоянной и временной нагрузок.
![]() = –1,414qa
+ 0,398qa = –1,016qa;
= –1,414qa
+ 0,398qa = –1,016qa;
![]() = –1,414qa
– 1,326qa = –2,740qa.
= –1,414qa
– 1,326qa = –2,740qa.
Таким образом, большее по модулю усилие в рассматриваемом стержне возникает при нагружении фермы постоянной нагрузкой и временной в положении 2. Если материал фермы одинаково хорошо работает на растяжение и сжатие
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.