Математика \ Математические задачи энергетики

Полная и расчетная диаграммы состояния объекта расчета надежности. Расчетные формулы показателей восстановления. Метод дифференциальных уравнений Колмогорова

Страницы работы

1 страница (Word-файл)

Фрагмент текста работы

19. Полная и расчетная диаграммы состояния объекта расчета надежности.

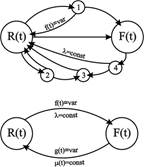Интегральная ф-ция распределения вероятности безотказной работы R(t) для произв-го, но фиксир-го момента времени t может рассматриваться как вер-сть пребывания объекта в состоянии безотказности от t=0 до t=tфикс.

Интегральная ф-ция распр-ния вер-сти отказа F(t), рассчитываемая для объекта, может рассматриваться как вероятность нахождения объекта в неработоспособном состоянии для момента времени от t=0 до t=tфикс.

Плотность распределения вероятности отказов f(t) для объекта может рассматриваться как переход объекта из работоспос-го состояния в состояние отказа за время от t=tфикс до t=tфикс+Δt.

Интенсивность отказов λ(t) может рассм-ся как переход объекта из работосп-го состояния в состояние отказа за Δt.

20. Количественные показатели восстановления.

Интегральная функция распределения вероятностей несвоевременного окончания ремонта S(t) - численно равна доле кол-ва элементов, подлежащих ремонту на момент t=0, не отремонтированных до произвольного, но фиксированного момента времени.

Интегральная функция распределения вероятностей своевременного окончания ремонта G(t) - численно равна доле кол-ва элементов, подлежащих ремонту на момент t=0, отремонтированных до произвольного, но фиксированного момента времени.

Поскольку S(t) и G(t) образуют полную группу несовместных событий , то для них справедливо: G(t)+S(t)=1 => G(t)=1-S(t) и S(t)=1-G(t).

Дифференциальная функция распределения вероятностей своевременного ремонта g(t) – численно равна среднему числу восстановлений в единицу времени на 1 объект из кол-ва объектов, подлежащих ремонту:

; ;

Интенсивность восстановления объектов μ(t)=[ед. времени ^-1 ]

21. Расчетные формулы показателей восстановления.

Аналитические взаимосвязи показателей восстановления.

Приняты следующие условия:

; ;

Таблица. Расчетные формулы показателей восстановления.

Если учесть, что интенсивности восстановления объектов величины постоянные и приняв соотношения таблицы (посл. столбец), S(t) может быть преобразовано:

(*)

Упрощения (*) на основе разложения экспоненты в ряд Тейлора недопустимы, т. к. численные значения интенсивности восстановления объектов систем достаточно велики, из-за чего замена экспоненты на прямую приводит к большой погрешности.

22. Метод дифференциальных уравнений Колмогорова.

В расчетах надежности объектов с большой интенсивностью отказов (соответственно с малым средним временем наработки на отказ tн) используются методы математической теории массового обслуживания. Объекты систем электроснабжения характеризуются малой интенсивностью отказа, большим tн на отказ, поэтому рассмотрим один метод – метод диф. уравнений Колмогорова. Диф. уравнения составляются по диаграмме состояний объекта в соответствии с правилом: количество уравнений равно кол-ву состояний объекта на диаграмме. В левой части каждого уравнения стоит производная вероятности состояния объекта. Правая часть содержит столько членов, сколько стрелок связано с данным состоянием. Если стрелка направлена из состояния – каждый член с «-», если в состояние – «+». Каждый член равен произведению интенсивности перехода, соответствующего данной стрелке, умноженного на вероятность того состояния, из кот. исходит стрелка (см. рис.).

(*)

Т. к. F(t) и R(t) связаны (F(t)+R(t)=1), то можно ограничится решением одного из уравнений Колмогорова. Решая 1-ое уравнение (*) при t=0, R(t)=1, F(t)=0 получим:

23. Логические схемы расчета надежности.

Системы электроснабжения образуют технологические схемы, имеющие определенное функциональное назначение. Логические схемы расчета надежности получаются из технологических на основе логических рассуждений, кот. ведут к цели расчета надежности.

Логические рассуждения бывают двух типов по отказу и по безотказу. Два их типа необходимы только для того, чтобы выбрать простейшую логическую схему (и простые расчетные соотношения). Практически используют два шаблона: по теореме умножения (союз И) и по теореме сложения (союз ИЛИ). Оба шаблона применимы к обоим типам логических рассуждений.

Логические рассуждения при составлении логических схем по технологическим схемам имеют обобщенный вид: система не откажет (откажет), если не откажет (откажет) этот ее элемент И(ИЛИ) тот, И(ИЛИ) этот и т. д.

24.Типовые логические схемы расчета надежности.

В этом случае используются характеристики: R – безотказность, F – отказ системы.

1. Обособленный элемент: R_Σ =R_{элемента}; F_Σ =F_{элемента}