Падение волны под углом на границу раздела двух сред

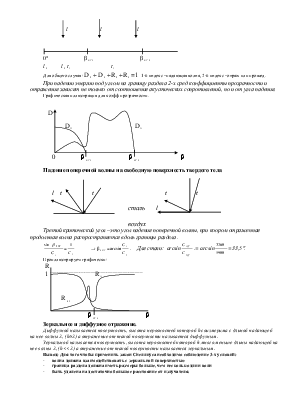
09.06.2004. В. Н. . Лекция 2.

Тема: Падение волны под углом на границу раздела двух сред.

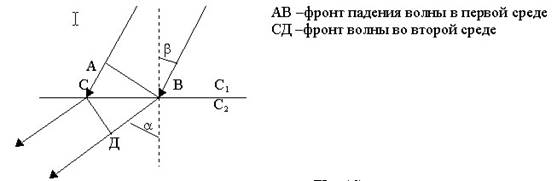
 Для сохранения равенства фаз время д б равно t==. Из равенства треугольников следует:

=;     =.

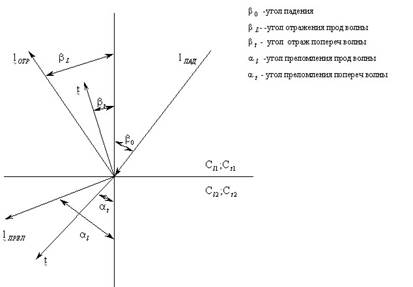
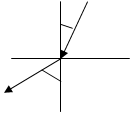
При падении волны под углом на границу падения имеют место 3 явления:

1). отражение (изменение направления распространения волны того же типа, что и падающая в первой среде),

2). преломление (изменение направления распространения волны того же типа, что и падающая во второй среде),

3). трансформация (появление волн другого типа, чем падающая, в первой и второй средах).

Отсюда запишем закон Снеллиуса:

Найти угол преломления, если ПЭП  П-121-2,5-50 установить на образец из меди.

Дано:                                                                    Найти:

b                                                      b

t                    сталь                                                               медь

       50                                                                           a-?

Применим закон Снеллиуса: =;      =Þ a=arcsinsin 50=0,71=32

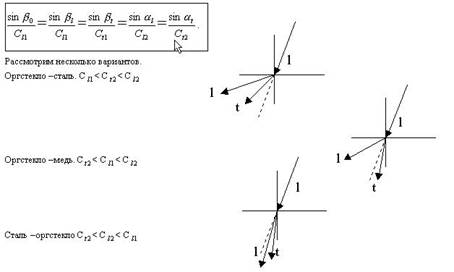
Две призмы с одинаковыми углами призм но из разного материала установлены на образец из одного и того же материала, причем a<a

Как соотносятся скорости распространения волн в материале призм?

                                                          Так как скорость распространения волны водном материале

                                                                    постоянна, то справедливо равенство:

                                                                     =; =или  т к b=bто =

a                     a                    отсюда следует  С> C

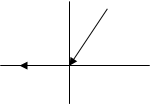
Первый критический угол.

b

l

l

Первый критический угол –это угол падения продольной волны, при котором продольная волна во второй среде распространяется вдоль границы раздела. Запишем закон Снеллиуса для данного случая:=: 1 –это sin90.   sinb=. Отсюда условием существования  первого критического является выражение:b· С< С.      b=arcsin  для стали: b(оргстекло-сталь)== arcsin=27°.

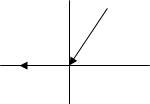
Второй критический угол.

                     b

l

t

Второй критический угол –это угол падения продольной волны, при котором поперечная волна во второй среде распространяется вдоль границы раздела.

=. Отсюда  условие существования второго критического угла: :b· С< С.

b=arcsin; для стали: b (оргстекло-сталь)== arcsin=55°.

Запишем коэффициент прозрачности D и отражения R для случая: С< C< C:

 

                l                       l                         l

0°                         b                                b

l         lt                             t

Для общего случая: D+ D+R+R=1  1-й индекс –падающая волна, 2-й индекс –отраж или прошед.

При падении энергии под углом на границу раздела 2-х сред коэффициенты прозрачности и отражения зависят не только от соотношения акустических сопротивлений, но и от угла падения.

Графическая иллюстрация для коэфф прозрачности.

 

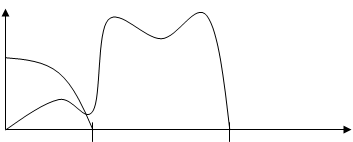   D

             D                                     D

     0                b                      b                        b

Падение поперечной волны на свободную поверхность твердого тела

 

     l    t                  t                                           t                  t

                                                   сталь       l

                                                   воздух

Третий критический угол –это угол падения поперечной волны, при коором отраженная продольная волна распространяется вдоль границы раздела.

=             Þ b=arcsin.     Для стали:  arcsin.= arcsin=33,5°.

Проиллюстрируем графически:

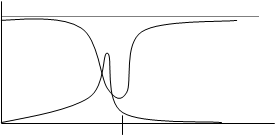 R

 1                            R

           R

                           b                            b

Зеркальное и диффузное отражение.

Диффузной называется поверхность, высота неровностей которой h соизмерима с длиной падающей на нее волны l, (h@l) а отражение от такой поверхности называется диффузным.

Зеркальной называется поверхность, высота неровностей которой h много меньше длины падающей на нее волны l, (h<<l) а отражение от такой поверхности называется зеркальным.

Вывод: Для того чтобы применить закон Снеллиуса необходимо соблюдение 3-х условий:

-  волна должна взаимодействовать с зеркальной поверхностью

-  граница раздела должна иметь размеры больше, чем несколько длин волн

-  быть удалена на достаточно большое расстояние от излучателя.