Расчет железобетонного монолитного лестничного марша (ширина марша – 1,4 м, высота – 1,65 м, ступени – 150х300 мм)

           2.1 Расчет лестничного марша

В данном проекте предусматриваются монолитные лестницы.

Железобетонный монолитный марш шириной 1,4 м, высота марша 1,65 м, ступени размером 150х300 мм. Конструктивное решение марша приведено на рисунке 1.

Бетон В15, арматура классов А240 и А400.

Расчетные данные для бетона В15:

-  расчетное сопротивление бетона сжатию R_B=8,5Мпа;

-  расчетное сопротивление бетона сжатию (для предельных состояний второй группы): R_B2=11,5 Мпа;

-  расчётное сопротивление бетона растяжению: r_bp = 0,75 Мпа;

-  расчётное сопротивление бетона растяжению (для предельных состояний второй группы): К_вр2⁼ 1,15 Мпа;

-  коэффициент условия работы: γ _B1= 1;

-  модуль упругости бетона:  Е_в = 23 ּ  10^-3 Мпа.

Расчётные данные для арматуры класса A240:

-  расчётное  сопротивление  арматуры растяжению  (при расчете сечений на действие изгибающих моментов): R_s= 225 Мпа;

-  модуль упругости арматуры: E_s = 21 ּ  10⁴ Мпа;

Расчётные данные для арматуры класса А400:

-  расчётное сопротивление арматуры растяжению (при расчете сечений на действие изгибающих моментов): R_s = 365 Мпа;

-  модуль упругости арматуры: E_s = 20 ּ  10⁴ Мпа;

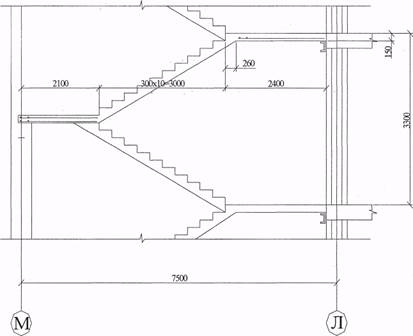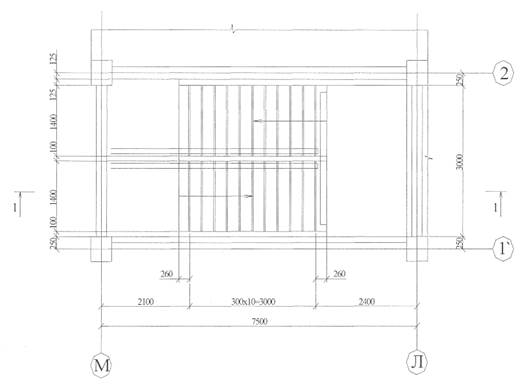
1-1

Рисунок 2.1 – Конструктивное решение лестницы

2.1.1 Определение нагрузок и усилий

Собственная    масса  марша    равна:    q^H==25 ּ  0,15=3,75кН/м² горизонтальной проекции.

Временная нормативная нагрузка для лестниц р^н=ЗкН/м².

Сбор нагрузки на 1 ног. м. лестничного марша приведён в таблице 1.

Таблица 2.1 - Сбор нагрузки на лестничный марш

Вид нагрузки	Нормативная нагрузка, кН/м2	Коэффициент надежности по нагрузке,    γf	Расчётная нагрузка, кН/м 2
Собственный вес qCB=qHּa=3,75ּ1,4 =6,3 кН/м	5,25	1,1	5,77
Временная нагрузка p врем = pH ּa =3ּ 1,4 = 4,2кН/м	4,2	1,3	5,46
Полная нагрузка Q = qCB+pврeм	9,45	___	11,23

Расчётная схема лестничного марша приведена на рисунке 2. Расчётная схема представляет собой балку, шарнирно опертую с одной стороны и жёстко защемлённую с другой. Балка загружена равномерно распределённой нагрузкой от собственного веса и полезной нагрузкой.

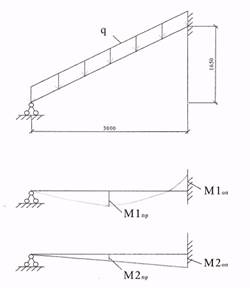
Рисунок 2.2 - Расчётная схема и эпюра моментов

М¹_on= qL²/8 = 11,23 ּ   3²/8 =12,63 кНּ м;

М¹_пр=М¹_оп/2= 12,63/2 = 6,32кНּ м.

Перераспределение моментов:

М²_оп=0,3М¹_оп = 0,3 ּ 12,63 = 3,79 кНּ м;

М²_пр= М²_оп/2 = 3,79/2 = 1,89 кНּ м;

М_оп =12,63-3,79 = 8,84 кНּ м.

Поперечная сила на опоре:

- жёсткая заделка

Q₁=3/8 ּ  q ּ L= 3/8 ּ 11,23 ּ 3 = 12,63 кН;

-шарнир

Q₁ = 5/8 ּ qּ L= 5/8 ּ 11,23ּ 3 = 21,06кН

2.1.2 Предварительное назначение размеров сечения марша

Назначаем:

-  толщину плиты (по сечению между ступенями) h_n = 30мм;

-  высоту рёбер h = 150мм;

-  толщину рёбер Ь_р = 80мм;

Действительное сечение марша заменяем на расчётное тавровое с полкой в сжатой зоне:

1)b = 2ּb_р=2ּ80 = 160мм;

2) ширину полки b_1p  при отсутствии поперечных рёбер принимаем не более   b¹_П=2ּ(L/6) + b = 2ּ(300/6) +16= 116см  или

b¹_п = 12h^l_n+ b = 12 ּ 3 + 16 = 52см.

За расчётное значение принимаем меньшее b¹_п = 52см.

Фактическое и приведённое поперечные сечения показаны на рисунке 3.

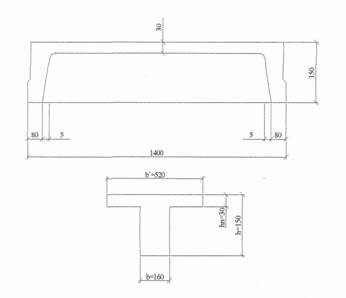
Рисунок 2.3 – Фактическое и приведенное сечение лестничного марша

  2.1.3 Подбор сечения продольной арматуры

Принимаем толщину защитного слоя бетона для нижней растянутой арматуры, а = 20 мм. Тогда h_o= h - а = 150 - 20 = 130мм =13см.

Расчёт производим в предположении, что сжатая арматура по расчёту не требуется.

Проверим условие:

М£ R_bּ b¹_n ּ h¹_n  ּ γ_В1 ּ(h₀-0,5ּ h¹_n),                                     (5)

884000 < 8,5 ּ 100 ּ 52 ּ 3ּ1ּ (13-0,5 ּ 3) = 1524900 Нּ см.

Условие выполняется, следовательно, граница сжатой зоны проходит в полке, и расчёт производим по формулам для прямоугольного сечения шириной b¹_n= 52см.

Вычисляем значение А₀:

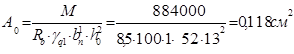                                                                (6)

По таблице 20 [10] находим η = 0,937; ξ = 0,1255;

Площадь сечения арматуры вычисляем по формуле:

                                            (7)

принимаем 2 диаметра 16 А400 с A_s=4,02см² . В каждом ребре устанавливаем по одному каркасу.

2.1.4 Расчёт наклонного сечения на поперечную силу

При расчёте элементов на действие поперечной силы должны соблюдаться два условия:

l.Q£0,3ּ φ_wl ּ φ_b1 ּ R_b ּ b ּ h₀,   [10, п.3.30]                                                     (8)

φ_w1 = 1,3;

φ_b1 = 1-b ּ  R_b = 1-0,01ּ 8,5 = 0,915, где b = 0,01 -для тяжелого бетона,

1)  12630 < 0,35ּ 8,5ּ100ּ  16ּ13 = 61880 Н;

2)  21060 < 0,35ּ8,5ּ100ּ16ּ13 = 61880 Н;

условие выполняется, принятые размеры сечения достаточны.

2. Q < φ_b3 ּ   R_Bp ּb ּh₀,                                                                                                      (9)

φ_b3 = 0,6 -для тяжелого бетона [10, табл. 21],

1)  12630 > 0,6ּ0,75ּ100ּ16ּ13=9360Н;

2)  21060 > 0,6ּ0,75ּ100ּ16ּ13 = 9360Н;

условие не выполняется, следовательно, требуется расчёт поперечной арматуры. По расчёту проектируем поперечную арматуру в 1/4 пролёта от шарнирной опоры и в 1/2 пролёта от жёсткой заделки, так как поперечная сила в сечении марша на расстоянии 1/4 и 1/2 пролёта равна:

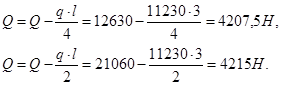                                                                  (10)

В средней части рёбер поперечную арматуру располагаем конструктивно с шагом 200мм.

В 1/4 и 1/2 пролёта назначаем из конструктивных соображений поперечные стержни диаметром 6мм A240 с шагом 75мм (не более h/2=150/2=75мм), А_х = 0,283см², R_ax=170Мпа. Для двух каркасов n=2, А_х=0,283ּ 2 = 0,566см².

Принятый шаг удовлетворяет условию

                                                   (11)

Вычисляем значение усилия, воспринимаемое поперечными стержнями на единицу длины рёбер марша [10]:

                                                               (12)

Поперечная сила, воспринимаемая бетоном и поперечными стержнями [7]:

                (13)

φ_b2 = 2 - для тяжелого бетона.

Прочность марша по наклонному сечению обеспечена.

 2.1.5 Расчет лестничного марша по деформациям

Сначала проверяем условие М^н £М_т [10, п.4.2], при соблюдении которого нормальные трещины в наиболее нагруженном сечении по середине пролёта не образуются.

Момент от полной нормативной нагрузки: М^н = М = 8,84 кНּм .

Момент трещинообразования М_т вычисляют:

M_T = R_врп ּ   W_T,                                                                                                                                            (14)

где, W_T = γּ W₀,  здесь γ = 1,75, по табл.29 [10];

                                                                                (15)

Для вычисления J_n и Y₀ площадь приведённого сечения:

A_n = A+A_s=bּ (h-h¹_n)+b¹_n ּ h¹_n+aּ A_s=16ּ(15-3)+52ּ 3 + 7,41ּ 4,02 = 377,8см²                (16)

Статический момент относительно нижней грани ребра:

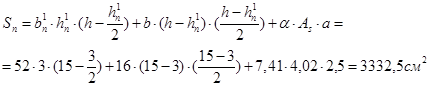                         (17)

Расстояние от центра тяжести приведённого сечения до нижней грани ребра:

                                                                              (18)

Момент инерции сечения относительно его центра тяжести:

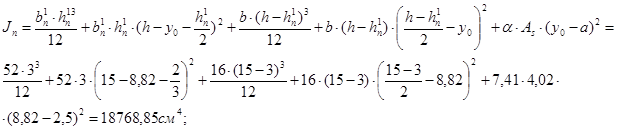(19)

W_T = γּW₀ =1,75ּ 2127,99=3724см³.

Момент трещинообразования:

M_T=R_BP2ּ W_T=1,15ּ  100ּ3724=4,28ּ10⁵Hּсм = 4,28 Hּм, что меньше М^н = 8,84 кНּм, следовательно, трещины в растянутой зоне сечения по середине пролёта образуется. Необходимо выполнить расчёт прогибов с учётом образования трещин в растянутой зоне. Кроме того, требуется проверка по раскрытию трещин.

Полная кривизна 1/р для участка с трещинами в растянутой зоне определяется:

                                                                      (20)

в этой формуле составляющие равны нулю.

Кривизна  от  непродолжительного  действия  полной  нагрузки определяется [10, п.4.15]:

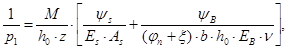                                                                 (21)

Где,  

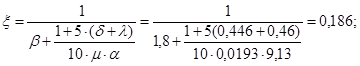[10, п.4.16]                                 (22)

здесь b=1,8 – коэффициент для тяжелого бетона

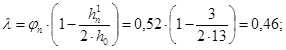                                                                  (23)

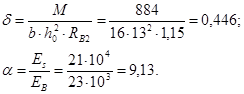                                                                          (24)

Значение z определяется:

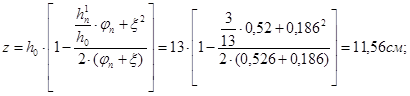                                         (25)

v — 0,45 - при непродолжительном действии нагрузки;

ψ_B= 0,9 - для тяжёлого бетона;

              ψ_S- коэффициент, определяемый по пункту 4.17 [10]: ψ_s = l,25-sּ m = 1,25-1,1ּ 0,31=0,91, здесь   s   -   коэффициент,   учитывающий   влияние   длительности действия