












ВВЕДЕНИЕ
B.I. СИСТЕМЫ СЧИСЛЕНИЯ
Для представления чисел в цифровых устройствах, а также для представления разнообразной информации в процессе программирования наряду с привычной для нас десятичной системой счисления широко используются другие. Рассмотрим принцип построения наиболее употребительных позиционных систем счисления.
Числа в таких системах счисления представляются последовательностью цифр (цифр разрядов), разделенных запятой на две группы: группу разрядов, изображающую целую часть числа, и группу разрядов, изображающую дробную часть числа:
... a2ala0, a-1a-2 ... (В.1)
Здесь а0, а1 , ... — цифры нулевого, первого и т. д. разрядов целой части числа, а-1 а-2, ... — цифры первого, второго и т. д. разрядов дробной части числа.
Единице каждого разряда приписан определенный вес рк, где р — основание системы счисления, k — номер разряда, равный индексу при буквах, изображающих цифры разрядов. Так. представленная выражением (B.I) запись озна-чает следующее количество:
![]()
Для представления цифр разрядов используется набор из р различных символов. Так, при р равном 10 (т. е. в обычной десятичной системе счисления) для записи цифр разрядов используется набор из десяти символов: 0,1, 2, ..., 9. При этом запись числа 729,32410 (здесь и в дальнейшем индекс при числе будет указывать основание системы счисления, в которой представлено число) означает следующее количество:
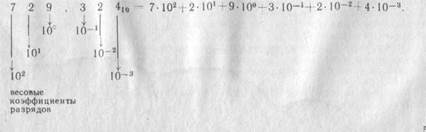
Используя такой принцип представления чисел, но выбирая различные значения основания р, можно строить разнообразные системы счисления.
Двоичная система счисления. Основание системы счисления р = 2. Таким образом, для записи цифр разрядов требуется набор всего лишь из двух символов, в качестве которых используются 0 и 1. Следовательно, в двоичной системе счисления число представляется последовательностью символов 0 и 1.
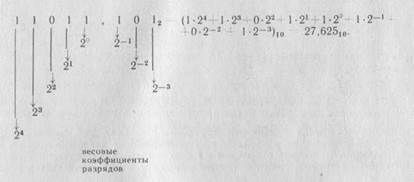
При этом запись 11011, 1012 соответствует в десятичной системе счисления следующему числу:
Восьмеричная система счисления. Основание системы счисления р 8. Следовательно, для представления цифр разрядов должно использоваться восемь различных символов, в качестве которых выбраны 0,1, 2,...,7 (заметим, что символы 8 и 9 здесь не используются и в записи чисел встречаться не должны). Например, записи 735, 468 в десятичной системе счисления соответствовало бы следующее число:

|
|
Хранение я-разрядных чисел в цифровой аппаратуре можно осуществить помощью устройств, содержащих п элементов, каждый из которых запоминает цифру соответствующего разряда числа. Наиболее просто осуществляется хра-нение чисел, представленных в двоичной системе счисления. Для запоминания цифры каждого разряда двоичного числа могут использоваться устройства с двум устойчивыми состояниями (например, триггеры). Одному из этих устойчивых со-стояний ставится в соответствие цифра 0, другому — 1 - цифра 1.
При хранении десятичных чисел каждая цифра десятичного числа предвари-тельно представляется в двоичной форме. Такая форма представления чисел но-сит название двоично-кодированной десятичной системы. Например, число 765,931о в двоично-кодированной десятичной системе представляется в следующем виде
![]()
Запоминание цифр 0 и 1 двоично-кодированного о десятичного числа можно осуществляться с помощью указанных выше элементов с двумя устойчивыми с состояниями.
Следует заметить, что несмотря на внешнее сходство двоично-кодированно десятичного числа (содержащего в разрядах лишь цифры 0 и 1) с двоичным числом, оно не является двоичным. В этом легко убедиться. Например, если целую часть приведенной выше записи в правой части равенства рассматривать к; двоичное число, то оно при переводе в десятичную систему счисления означа. бы 189310, что не совпадает с целой частью исходного числа 765.
Рассмотренный способ двоичного представления (кодирования) десятичного цифр использует так называемый код 8421 (название кода составлено из весов коэффициентов разрядов в двоичной системе счисления).
В.2. ПЕРЕВОД ЧИСЕЛ ИЗ О ОДНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ДРУГУЮ
Основания восьмеричной и шестнадцатеричной систем счисления выражают целой степенью двух (8=23; 16=24). Этим объясняется простота преобразован чисел между этими системами
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.