4. Управление передается в основной блок программы T_InterAction, где проверяется условие прорезания льда по времени. Т.е. dt>0, если прорезание есть, тогда определяется скорость продвижения льда, как V=dx/dt, если прорезания нет, то скорость движения льда V=0. Если Tf>0, т.е. прорезание есть, тогда рассчитывается количество циклов нагружения, как Nf=t/Tf, если прорезания нет, то Tf=0 и выходят из программы.
5. Оформление промежуточных результатов их непосредственная печать выполняется в процедуре оформления EndShowResult.
Процедура Proc_MoveIce, моделирующая процесс взаимодействия льда с опорой:
1. В эту программу входит блок расчета непосредственного контакта передней льдины и опоры гидротехнического сооружения ContactIceConstr. На выходе из программы определяется площадь ушедшего льда ArOut и его масса mOut=ArOut*H_Ice*D_Ice, пересчитывается линейный размер льда перед опорой ll=ll-dx, который становится меньше на длину прорезания льда опорой; площадь льда перед опорой A=A-ArOut и масса льда перед опорой m=m-mOut, которые становятся меньше на величину ушедшего льда, и определяется длина льда за опорой l=l+dx, который увеличивается на длину прорезания.
2. Если выполняется условие скола льда l<4*R_Con, т.е. длина льда перед опорой еще меньше, чем два диаметра опоры и льдина скололась, или mOut>m0, т.е. масса ушедшего льда больше, чем масса одной льдины, или A£0, т.е. перед опорой нет льда, то тогда из системы ушла одна льдина и количество льда перед опорой стало меньше nIce=nIce-k, а количество льда ушедшего больше nOut=nOut+k, далее опять пересчитывают длину льда перед опорой, массу и площадь льда перед опорой, а также длину льда за опорой, массу и площадь льда за опорой.
3. Если же льдина еще не скололась, то текущее время прорезания T_i увеличивается на интервал по времени T_i=T_i+dt и выходят из программы.
Процедура непосредственного контакта передней льдины и опоры гидротехнического сооружения ContactIceConstr.
1. В процедуре FunForce определяется сила взаимодействия льда с опорой.
2. Проверяется наличие движения льда.
2.1. Если льдина движется V>0, тогда определяется параметр W1=2*H_Ice*Sqr(D_Ice*A*Rb)
– сила удара, и параметр W=Rightside=Ec/W, что представляет собой правую
часть в интегральном балансовом соотношении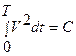 
(см. постановку задачи),
вычисляется глубина внедрения льда в опору из условия (7). Переход на процедуру
L0, в которой формируется модель изменения скорости продвижения льда (ModelVelocity).
2.2. Если же движения льда нет, т.е. V=0, тогда dx=0 (глубина прорезания равна нулю) и параметр W1=0 (сила удара равна нулю).
3. Проверяется энергетическое условие остановки льда Fs*StepR<EnC(i).
3.1. Если энергии льда недостаточно, чтобы льдина прорезалась на шаг SrepR, т.е. лед перед опорой стоит и ждет пока не подойдет следующая льдина и не передаст свой дополнительный импульс, тогда выходят из программы ContactIceConstr и возвращаются в Proc_MoveIce.
3.2. Если же энергии достаточно для прорезания льда, тогда организуется цикл расчетов продвижения льда на величину StepR от i до NumAr-1, т.е. глубина прорезания dx увеличивается на шаг прорезания льда опорой dx=dx+StepR.
4. Проверяется условие, чтобы расчетная глубина прорезания не была больше линейного размера льда за опорой (dx>l).
4.1. Если условие выполняется, т.е. вся льдина уже прорезалась, то dx=l, а скорость прорезания обнуляется.
4.2. Если же не все льдины еще прорезались, тогда определяется энергия необходимая для прорезания льда на величину dx, как W=Fs*dx.
5. Проверяется энергетическое условие движения льда W<EnC(i+1).
5.1. Если энергии от действия силы льда не достаточно для того, чтобы прорезался лед перед опорой (движения нет), тогда выполняется процедура L0.
5.2. Если же энергии достаточно для прорезания льда, т.е. W=EnC(i+1), тогда идут на следующий шаг расчетов Next i.
6. Организация процесса скола льда опорой. Весь процесс делится на два этапа: 1) если льдина еще не прорезалась на диаметр опоры; 2) если она уже прорезалась на величину больше, чем диаметр опоры, т.е. dx>2*R_Con.
6.1. В первом случае площадь ушедшего льда определяется по формуле (8).
6.2. Во втором случае по формуле (9).
Программа моделирования скорости внедрения льда в опору ModelVelocity.
1. На первом этапе решения задачи определяется максимально возможная скорость подхода льда к опоре по формуле VelocityMax=V_Ice/dVelocity.
2. Выбирается модель изменения скорости: Cas0 – перевернутая вниз парабола, Cas1 – выпуклая степенная парабола.
2.1. В зависимости от выбранного случая изменения скорости в программе рассчитывают глубину прорезания (dx) и время прорезания льда опорой (dt). Именно это текущее время прорезания льда опорой используется во всех дальнейших программах расчета (см. рис. 1).
Блок-схема расчета истирающего воздействия на опоры сооружения дрейфующим ледяным покровом представлена на рис.3.3.
Рис. 3.3. Блок-схема расчета истирающего воздействия на опоры сооружения
дрейфующим ледяным покровом
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.