Многоцикловое и истирающее воздействия дрейфующего ледяного покрова на морские гидротехнические сооружения (Воздействие ледяного покрова на Инженерные сооружения континентального шельфа), страница 5

Расчет функции распределения усталостной долговечности можно упростить, если пренебречь вариациями величины m - характеристика угла наклона кривой усталости, что вполне допустимо. Расчет непосредственно по формуле (1.12) во многих случаях бывает затруднен вследствие того, что нет амплитуд s_ai, превышающих s_-1Д, т.е. s_amax<s_-1Д, и лишь за счет случайных вариаций s_-1Д и s_amax возможно появление амплитуд, превышающих s_-1Д. В этом случае сумма в знаменателе (1.12) обращается в ноль и расчет теряет смысл. Для преодоления этой трудности вводится коэффициент, характеризующий относительный уровень переменной нагрузки, определяемый по формуле:

,                                                   (1.13)

С учетом этого обозначения получаем:

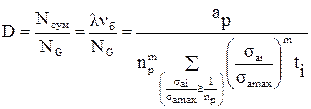,              (1.14)

где N_сум=ln_б - суммарное число циклов за срок службы; D=N_сум/N_G - относительная долговечность. Как уже говорилось, вариациями а_р и суммы, стоящей в знаменателе (1.14) можно пренебречь. Тогда рассеяние относительной долговечности Nс_ум/N_G получается за счет случайных вариаций s_-1Д (характеристика материала) и s_amax (характеристика нагружения), входящих в n_р.

При заданном Nс_ум/N_G  и соответствующем ему по (1.14) значению n_р условие появления усталостной трещины имеет вид

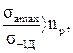   при   ,                  (1.15)

Если величины s_amax и s_-1Д распределены нормально со средним значением s^ср_amax и s^ср_-1Д и коэффициентами вариации n_samax=n_а и некоррелированы, то величина М также распределена нормально со средним значением М^ср и дисперсией S²_М, определяемым по формулам:

,                                             (1.16)

,                                             (1.17)

где S²_s-1Д, S²_samax - дисперсия величин s_-1Д и s_amax, соответственно.

Значение М_р, соответствующее вероятности Р, определяется по формуле:

,                                                 (1.18)

Далее находят вероятность появления трещины из условия

,                                        (1.19)

откуда 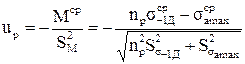,                                                           (1.20)

Введем обозначения

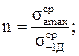
   ,                                    (1.21)

Коэффициентом вариации предела выносливости детали n_s-1Д называют отношение среднеквадратичного отклонения предела выносливости S_s-1Д к среднему значению предела выносливости детали на множестве всех плавок данной марки s^/ср_-1Д, т.е.

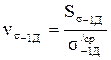,                                            (1.22)

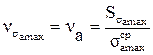,                                    (1.23)

С учетом выражений (1.21) и (1.22) из данной формулы получаем

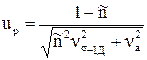,                                     (1.24)

где - относительный коэффициент запаса.

По формуле (1.24) строится функция распределения относительной долговечности D=N_сум/N_G в такой последовательности: для ряда значений D находят n_p по формуле (1.14), далее величины - n и  по (1.21), квантиль u_p - по (1.24) и соответствующему ей вероятность разрушения р - по табл.1.3 [ ].

В случае необходимости учесть рассеяние величин n_б и N_б можно поступить следующим образом. Из (1.14) можно записать

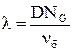   или   ,               (1.25)

Практика показывает, что величина lgl может быть принята распределенной по нормальному закону. В это случае значение усталостной долговечности, выраженной в числе блоков и соответствующей вероятности разрушения Р, может быть найдено по уравнению

,                                (1.26)

где u_p - квантиль нормального распределения, соответствующая вероятности Р. Величина lg^cpl находится по формуле:

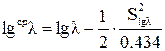,                                 (1.27)

где l находится по (1.24), при u_p=0. Уравнение (1.14) используется при наличии горизонтального участка кривой усталости.

Если кривая усталости имеет два наклонных участка, то она описывается уравнением, при s_amax ³ s_-1Д:

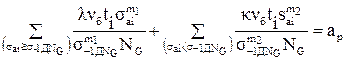.       (1.28)

После простых алгебраических преобразований с учетом N_сум=ln_б получаем (1.29). При s_amax<s_-1ДNG первое слагаемое в квадратной скобке отсутствует. Из (1.14) получаем

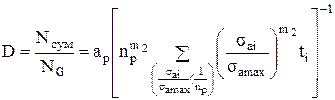,         (1.29)