Проектирование турбины для привода генератора мощностью 15 МВт и с частотой вращения 3000 об/мин, страница 5

По известным значениям:

h_o=2989,49кДж/кг – энтальпия пара перед первой ступенью;

P_o=18бар – давление пара перед первой ступенью;

t_o=283°С – температура пара перед первой ступенью;

v_o=0,138м³/кг – удельный объем пара перед первой ступенью;

Dh_o=40кДж/кг располагаемый теплоперепад ступени.

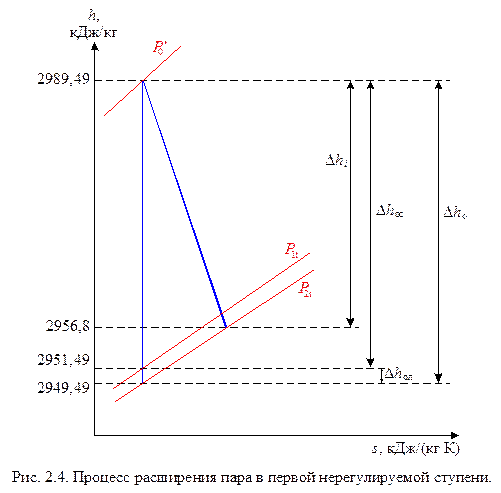
Построив процесс расширения пара в первой нерегулируемой ступени (рис. 2.4) из hs-диаграммы определяем параметры пара при теоретическом расширении:

после ступени – h_2t=2949,49кДж/кг; v_2t=0,15549м³/кг; Р_2t=15,1бар; t_2t=262°С;

после сопловых лопаток – h_1t=2951,49кДж/кг; v_1t=0,15324м³/кг; Р_1t=15,5бар; t_1t=265°С.

Теплоперепад на лопатках первой нерегулируемой ступени:

38кДж/кг

2кДж/кг

2.2.2 Определение размеров первой нерегулируемой ступени.

Фиктивная скорость в ступени

282,84м/с

Принимаем угол выхода из сопловой решетки 12°

Задавшись скоростным коэффициентом сопел j=0,96, определяем оптимальное соотношение скоростей:

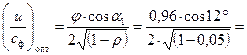0,48

Откуда следует что окружная скорость потока в первой нерегулируемой ступени:

135,76м/с

Определяем средний диаметр ступени

0,864м

Теоретическая скорость выхода пара из сопел

275,68м/с

Для определения площади выходного сечения сопловой решетки необходимо определить режим работы соплового аппарата, который зависит от отношения давлений:

0,861>0,546,

Следовательно, истечение пара – докритическое и сопла должны быть суживающимися.

Площадь выходного сечения сопел:

где:   m_c=0,97 – коэффициент расхода сопел [1 стр.32]

11143мм².

Высота сопловой лопатки

где:   e – степень парциальности, принимаем e=0,9

22мм

Приняв хорду профиля сопловой лопатки b₁=50мм, уточняем коэффициенты:

0,962

0,971

Коэффициенты мало отличаются от принятых.

2.2.3 Определение скоростей пара в первой нерегулируемой ступени.

2.2.3.1Действительная скорость пара на выходе из сопел.

264,65м/с

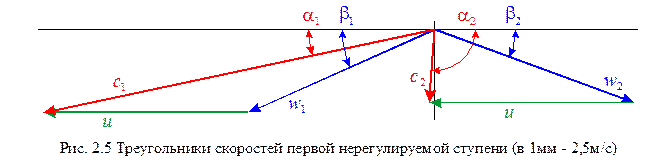
Строим треугольник скоростей на выходе из сопловой решетки (рис. 2.5) и из треугольника определяем:

угол входа в рабочую решетку b₁=24,1°

скорость на входе в рабочую решетку w₁=134,8м/с

2.2.3.2 Теоретическая скорость на выходе из рабочих лопаток.

148,94м/с

Приняв величину перекрыши Dl₂=3мм, определяем высоту рабочей лопатки

l₂= l₁+ Dl₂=22+3=25мм.

Задавшись хордой профиля рабочих лопаток b₂=40мм, находим скоростной коэффициент рабочей решетки y=0,945. Тогда действительная относительная скорость на выходе из рабочих лопаток:

140,75м/с

Выходной угол из рабочих лопаток

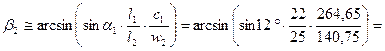20,1°

Строим треугольник скоростей на выходе из рабочей решетки (рис. 2.5) и из треугольника определяем:

угол выхода абсолютной скорости из рабочей решетки a₂=94,3°

абсолютная скорость на выходе из рабочей решетки с₂=48,54м/с

2.2.4 Определение КПД и внутренней мощности первой нерегулируемой ступени.

2.2.4.1 Относительный лопаточный КПД ступени.

где:   ; ;  – потери энергии соответственно в соплах, в рабочих лопатках, с выходной скоростью.

Потери энергии в соплах:

2,98кДж/кг

Потери энергии в рабочих лопатках:

1,19кДж/кг

Потери энергии с выходной скоростью:

1,178кДж/кг

Относительный лопаточный КПД ступени.

0,87

2.2.4.2 Внутренний относительный КПД первой нерегулируемой ступени.

Кроме потерь на облопачивание в ступени имеются дополнительные потери:

Потери на трение

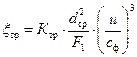
где:   К_тр – коэффициент трения, принимаем =0,47·10^–3

0,0035

Потери в диафрагменных лабиринтовых уплотнениях

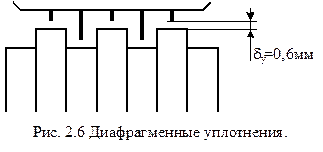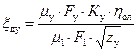
где:   м2 – площадь кольцевого зазора  (рис. 2.6)

 – коэффициент, учитывающий сужение зазора в уплотнении, принимаем 0,7

 – коэффициент,учитывающий протечки по гладкому валу (в данном случае он равен 1)

 – число гребешков, принимаем равное 5

0,0189

Потери на протечки поверх бандажа

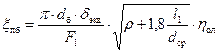
где:   d_экв=3,98·10^–4м – эквивалентный зазор над бандажом

0,889м – диаметр бандажа

0,0267