





























Тепломассообмен
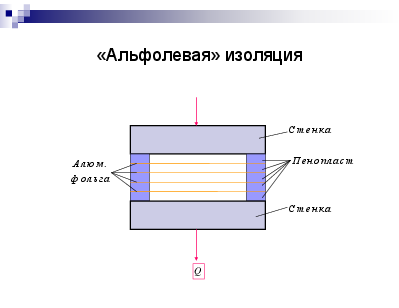
«Альфолевая» изоляция
![]()
![]()
![]()
![]()
Термическое сопротивление тепло- передачи через изолиров-й трубопровод
(1)
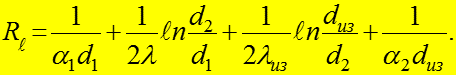
При
(остальные величины постоянные):
![]()
(2)


(3)
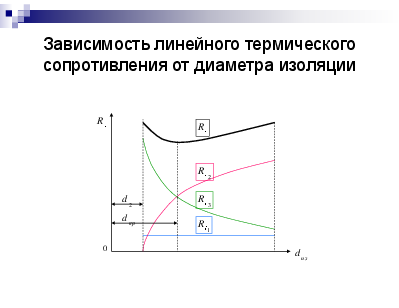
Из (3) видно, что растет с увеличением
![]()
![]()
а
- уменьшается (см.следующий слайд).
![]()
Зависимость линейного термического сопротивления от диаметра изоляции
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Исследование функции на минимум
соответствует максимум теплопотерь. Для определения
![]()
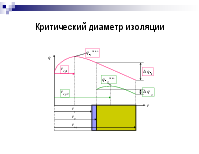
критического диаметра изоляции надо исследовать функцию (3) на минимум:
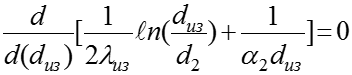
или:
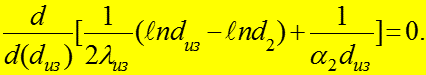
При с учетом, что
![]()
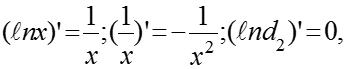
имеем:
Эффективность тепловой изоляции трубопроводов
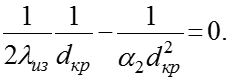
После сокращения на имеем:
![]()
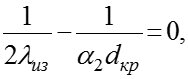
или:
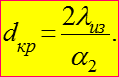
откуда:
![]()
При
- эффективная изоляция;
![]()
при
- малоэффективная изоляция.
![]()
Действительно, из следующего слайда:
![]()
Критический диаметр изоляции
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Теплопроводность в стержне (ребре) постоянного поперечного сечения
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Условные обозначения
- поперечное сечение стержня,
![]()
![]()
- периметр стержня, м;
![]()
- температура окружающей среды,
![]()
![]()
- коэффициент теплоотдачи,
![]()
![]()
- температура стержня,
![]()
![]()
- температура основания стержня,
![]()
![]()
- избыточная температура стержня, К;
![]()
- избыточная температура основания стержня, К;
![]()
- длина стержня, м.
![]()
![]()
Уравнение теплового баланса
(бесконечный стержень).
![]()
Уравнение теплового баланса:
,
(1)
![]()
где
- теплота, отдаваемая конвекцией окружающей жидкости;
![]()
- теплота, подведенная т-проводностью к левой грани;
![]()
- теплота, отведенная т-проводностью от правой грани.
![]()
По закону Фурье для теплопроводности:
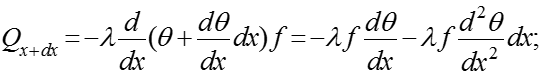
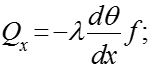
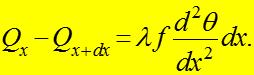
(2)
Конвективный тепловой поток к окружающей жидкости по уравнению Ньютона-Рихмана:
![]()
где
![]()
Дифференциальное уравнение для избыточной температуры в стержне
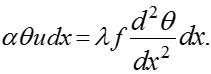
После сокращения на для избыточной температуры в стержне:
получаем дифференциальное ур-е
![]()
(4)
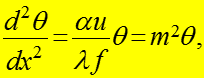
где
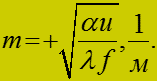
Для
![]()
при постоянном сечении ребра, тогда интеграл от (4):
(5)
![]()
Константы интегрирования определяются из граничных условий для конкретных случаев. Рассмотрим их далее.
А) Стержень бесконечной длины
![]()
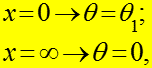
(6)
так как при вся теплота будет отдана жидкости.
![]()
(7) (8) (9)
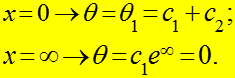
Подставляем (6) в (5): при
Из (8):
![]()
![]()
Подставляем значение константы (9) в (7):
(10)
то есть
![]()
![]()
После подстановки констант интегрирования (9) и (10) в (5):
(11)
![]()
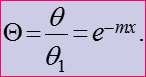
Или безразмерный избыток температуры:
(12)
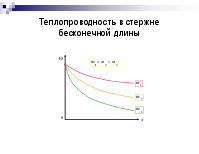
Теплопроводность в стержне бесконечной длины
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Теплота, отданная стержнем жидкости
все кривые
![]()
асимптотически приближаются к 0. Из следует, что m пропорциональна теплоотдаче с боковой поверхности и обратно пропорциональна
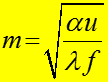
теплопроводности вдоль стержня, то есть надо выбирать материал для ребер с большим
. Теплота, отданная стержнем жидкости
![]()
равна теплоте, прошедшей через его основание, Вт:
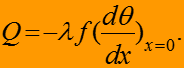
(13) Из (11) следует:
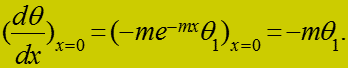
(14)
(14) в (13):
(15)
![]()
Б) Стержень конечной длины
(16)
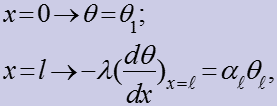
При теплота, подведенная теплопроводностью к концу стержня, равна конв.теплоотдаче от конца стержня к жидкости. Из (16) следует:
![]()
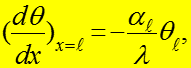
(17)
где коэффициент теплоотдачи от конца стержня; Избыточная температура на конце стержня.
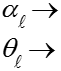
Если подставить граничные условия (16) в общее решение диф. ур-я (5) и найти константы интегрирования
![]()
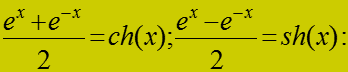
то с учетом обозначений:
Избыточная температура в стержне конечной длины
Если теплоотдачей с торца пренебречь
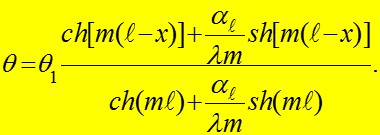
то
(18)
![]()
граничные условия будут: при
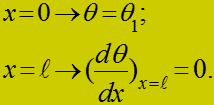
(19)
Это возможно при малом и большом,
![]()
![]()
то есть при тогда вместо (18):
![]()
(20)
Обычно доля теплоты, отдаваемой с торца, мала по сравнению с таковой с боковых
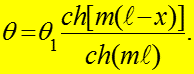
поверхностей, поэтому для практических расчетов использ-ся ур-е (20). Так как в нем только остальные величины постоянные, то
![]()
с учетом, что имеем:
![]()
Теплота, отданная стержнем жидкости
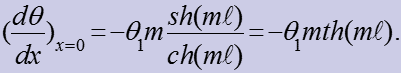
(21)
Подставляем (21) в (13), получаем теплоту, отданную стержнем жидкости, равную теплоте, прошедшей через его основание, Вт:
(22)
![]()
или с учетом, что
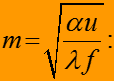
(23)
![]()
![]()
Тогда формулы (22) и (23) для конечного стержня переходят в в уравнение (15) для бесконечного стержня.
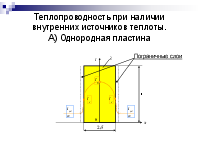
Теплопроводность при наличии внутренних источников теплоты. А) Однородная пластина
Пограничные слои
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Дифференциальное уравнение теплопроводности
бесконечная пластина; в стационарном процессе:
![]()
Найти:
![]()
![]()
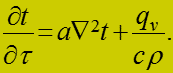
(1)
Дифференциальное уравнение теплопроводности:

Для стационарного процесса тогда:
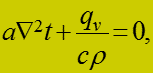
(2)
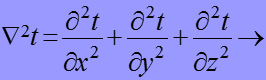
где оператор Лапласа.

При

тогда после деления (2) на дифференциальное уравнение теплопроводности в бесконечной пластине:
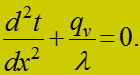
(3)
Граничные условия
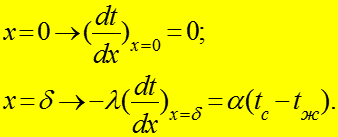
(4)

Интегрируем (3):
(5) разделяем переменные:

После 2-го интегрирования:
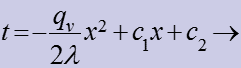
уравнение параболы. (6)
Константы интегрирования
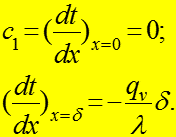
(7) (8)
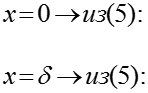

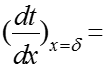
Подставляем (8) в (4):
(9)
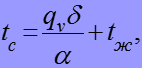
(10)
После сокращения на
![]()
подставляем (10) в (6) при с учетом, что
![]()
![]()
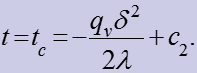
Приравнивая (10) и (11), получим:
(11)

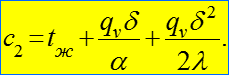
(12)
откуда:
Тепловые потоки и температуры
то есть температура в пластине изменяется по параболич.закону.
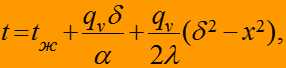
(13)
(14)
то есть
![]()
![]()
Если температура стенки известна или вычислена по уравнению (10), то есть заданы граничные условия I рода, то:
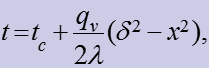
(15)
тогда при
![]()
(16)
- температура в центре пластины.
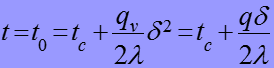
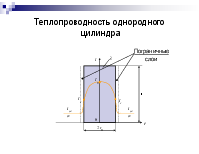
Теплопроводность однородного цилиндра
Пограничные слои
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Дифференциальное уравнение теплопроводности в полярных координатах
бесконечный цилиндрический стержень.
![]()
Для стационарного процесса
![]()
Найти
![]()
Условия теплоотдачи с правой и левой сторон одинаковы (симметри- чная задача), следовательно можно рассматривать только правую по- ловину цилиндра. Дифференциальное уравнение теплопроводности:
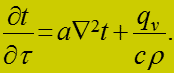

(1)
Для стационарного процесса тогда:
где оператор Лапласа в полярных (цилиндрических) координатах:

(2)
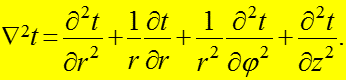
(3)
Граничные условия


тогда после деления (2) на получим дифференциальное уравнение теплопроводности для бесконечного цилиндра при стаци- онарном режиме:
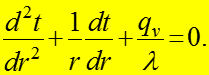
(4)

Граничные условия: при
(5)
Найти:
![]()

(6)
После двойного интегрирования (4) имеем:
Теплота, отданная конвекцией от цилиндра к окружающей его жидкости
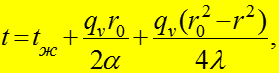
(7)
то есть температура в цилиндре изменяется по параболическому закону.

Температура на оси цилиндра при
(8) (9)
![]()

на стенке цилиндра при
![]()
![]()

Плотность теплового потока из (9),
(10)
![]()
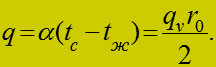
(11)
Полная теплота:
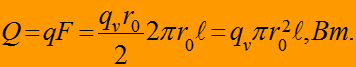
(12)
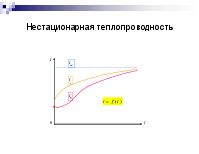
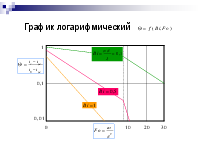
Нестационарная теплопроводность
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Дифференциальное уравнение теплопроводности
температуры в центре тела и на его
![]()
![]()
поверхности. Процесс описывается дифференциальным уравне- нием теплопроводности без внутренних источников теплоты
![]()
Условия однозначности: 1) Геометрические - геометрические
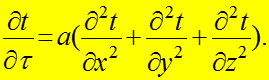
(1)
размеры и форма тела; 2) Физические – физические параметры тела; 3) Начальные - при
4) Граничные
![]()

Решение заключается в условия III рода нахождении функции
![]()
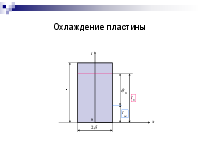
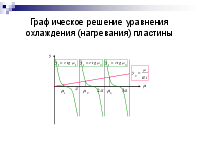
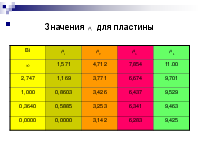
Охлаждение пластины
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Дифференциальное уравнение, начальные и граничные условия
![]()
В дифференциальное уравнение и граничные условия подставим избыточную температуру
Для бесконечной пластины
![]()

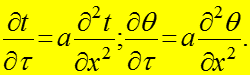
тогда:
(2)
![]()
Начальные условия: при
(3)
![]()
При симметричная задача, тогда граничные условия:
![]()
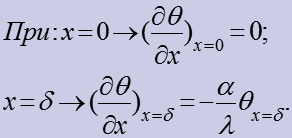
(4)
Разделение переменных
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.