Наносекундный сильноточный разряд в сверхзвуковом потоке газа, страница 3

где     и     - поперечные (по отношению к вектору электрического поля) размеры разрядной области, N_e(r) и      - пространственные распределения концентрации и подвижности электронов в направлении (0-L₁) здесь        определяется распределением плотности газа. Вдоль оси (0-L₀) распределение параметров считалось однородным.

Динамика   температуры   газа   описывалась уравнением:

где - удельная теплоемкость газа при постоянном объеме, - коэффициент теплопроводности воздуха, - среднее количество колебательных квантов на молекулу N₂,    - характерное время VT-релаксации колебательного возбуждения N₂(v), - скорость нагрева газа в химических реакциях.

Для описания источника нагрева за счет химических реакций использовалась модель, которая включает реакции диссоциации сильновозбужденных электронных состояний кислорода (заселяемых либо электронным ударом, либо при тушении возбужденных состояний N₂), реакции тушения возбужденных атомов молекулами азота и др.

Расчетная область ограничивалась зоной действия разряда 0 < г < L₁. Граничные условия для уравнений (1), (3) и др. выбирались исходя из предположения о невозмущенных параметрах газа при  г = 0 (перед УВ) и параметрах, определяемых соотношениями Гюгонио при r = L₁(за фронтом УВ).

Далее приводятся результаты расчетов воздействия импульсного самостоятельного разряда на воздух, по которому предварительно прошла ударная волна заданной интенсивности. Начальное давление газа составляло Р₀ = 20 Тор. Для описания параметров разряда использовалась экспериментально измеренная (рис. 3) зависимость тока разряда от времени. При заданном числе Маха параметры газа за УВ в момент воздействия разряда (давление Р₁, концентрация N₁и температура Т₁) определялись с использованием соотношений Гюгонио. Соответствующие значения приведены в таблице.

При размерах электродов исследуемой разрядной системы L₀ = 4.8 см, L₁= 10 см  и давлениях Р   20 Тор характерные частоты диффузионных процессов для заряженных частиц составляют:

(D_a - коэффициент амбиполярной диффузии), что много меньше обратного времени разрядного импульса и характерных частот реакций электрон-ионной рекомбинации. Таким образом, пространственная (в направлении, поперечном вектору электрического поля) динамика заряженных частиц в рассматриваемых условиях несущественна и при однородном начальном распределении плотности газа задача моделирования разряда может рассматриваться в нульмерном приближении. Как уже отмечалось, одномерная расчетная модель использовалась при рассмотрении пространственно неоднородного начального распределения плотности газа: при движении по разрядному промежутку УВ.

На рис. 4 отражены результаты расчета динамики концентрации электронов и приведенного электрического поля E/Nв исследуемом разряде в воздухе (Р₀ = 20 Тор, Т₀ = 300 К) за ударной волной с числом Маха М = 2. Средняя по времени величина приведенного поля в разряде составляет примерно E/N   100 Td. Расчетное значение энерговклада достигает 0.037 эВ/мол, что согласуется с экспериментальными оценками.

Параметры газа за ударной волной и энерговклад в разряд в зависимости от числа Маха

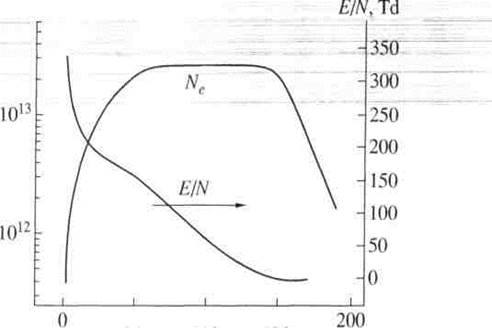                   Концентрация, см ^-3

Время, нс

Рис. 4. Динамика концентрации электронов и приведенного электрического поля E/Nв разряде в воздухе

В таблице представлены расчетные значения максимальных энерговкладов в разряд для различных значений числа Маха УВ. Данные значения отличаются незначительно и лежат в диапазоне       0.035-0.039 эВ/мол. При этом изменения температуры газа за время действия разряда не превышают 20 К.