Применение определенного интеграла в задачах физики
№1
Котел имеет форму параболоида вращения. Радиус основания ![]() м,
глубина котла
м,
глубина котла ![]() м.
Он наполнен жидкостью, плотность которой
м.
Он наполнен жидкостью, плотность которой ![]() .
Вычислить работу, которую нужно произвести, чтобы выкачать жидкость из котла.
.
Вычислить работу, которую нужно произвести, чтобы выкачать жидкость из котла.
Решение
Из курса физики известно, что работа ![]() ,
где
,
где ![]() –
сила, действующая на материальную точку, которую перемещают на расстояние
–
сила, действующая на материальную точку, которую перемещают на расстояние ![]() .
Однако предположение о том, что для данной задачи
.
Однако предположение о том, что для данной задачи ![]() ,
где
,
где ![]() –
вес жидкости, будет ошибочным. Например, чтобы выкачать каплю жидкости с
глубины 1 м, и выкачать каплю той же самой массы с глубины 1 см, необходимо
произвести разную работу. Поэтому в данном случае необходимо искать другой путь
решения, который бы учитывал изменение работы с каждой выкачанной каплей воды.
–
вес жидкости, будет ошибочным. Например, чтобы выкачать каплю жидкости с
глубины 1 м, и выкачать каплю той же самой массы с глубины 1 см, необходимо
произвести разную работу. Поэтому в данном случае необходимо искать другой путь
решения, который бы учитывал изменение работы с каждой выкачанной каплей воды.
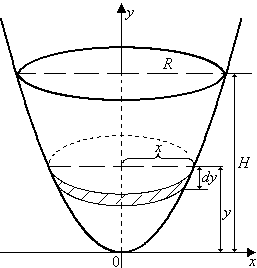 Введем систему координат так, как показано
на рисунке.
Введем систему координат так, как показано
на рисунке.
Рассмотрим тонкий слой воды, лежащий на глубине ![]() .
Полагаем, что данный слой настолько тонок, что толщиной его можно пренебречь.
Тогда, для того, чтобы выкачать все точки этого слоя придется затратить
одинаковую работу, т.к. весь слой лежит на одной глубине. Обозначим толщину
слоя
.
Полагаем, что данный слой настолько тонок, что толщиной его можно пренебречь.
Тогда, для того, чтобы выкачать все точки этого слоя придется затратить
одинаковую работу, т.к. весь слой лежит на одной глубине. Обозначим толщину
слоя ![]() .
Так как высота слоя очень мала, полагаем, что его объем равен объему прямого
цилиндра с радиусом основания
.
Так как высота слоя очень мала, полагаем, что его объем равен объему прямого
цилиндра с радиусом основания ![]() ,
а высотой
,
а высотой ![]() .
Погрешностями, возникающими при такой замене, пренебрегаем ввиду малой толщины
слоя.
.
Погрешностями, возникающими при такой замене, пренебрегаем ввиду малой толщины
слоя.
Тогда ![]() ,
где
,
где ![]() –
искомый объем. Далее необходимо перейти к одной переменной:
–
искомый объем. Далее необходимо перейти к одной переменной: ![]() или
или
![]() .
Учтем то, что форма котла – параболоид вращения, т.е. в сечении плоскостью ХОУ
получим параболу, уравнение которой
.
Учтем то, что форма котла – параболоид вращения, т.е. в сечении плоскостью ХОУ
получим параболу, уравнение которой ![]() .
Данная парабола проходит через точку
.
Данная парабола проходит через точку ![]() ,
поэтому
,
поэтому ![]() ,
,
![]() ,
,
![]() .
Подставляя найденное значение в формулу для
.
Подставляя найденное значение в формулу для ![]() ,
получим
,
получим ![]() .
Далее,
.
Далее, ![]() ,
где
,
где ![]() –
масса выделенного слоя. Так как вес слоя
–
масса выделенного слоя. Так как вес слоя ![]() ,
то работа
,
то работа ![]() по
извлечению слоя веса
по
извлечению слоя веса ![]() из
глубины
из
глубины ![]() составит
составит
![]() .
Учитывая то, что
.
Учитывая то, что ![]() ,
получим
,
получим
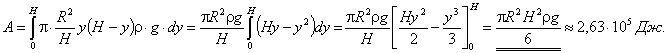
№2
Треугольная пластинка, основание которой ![]() ,
высота
,
высота ![]() ,
вращается вокруг своего основания с постоянной угловой скоростью
,
вращается вокруг своего основания с постоянной угловой скоростью ![]() .
Найти кинетическую энергию пластинки, если толщина ее равна
.
Найти кинетическую энергию пластинки, если толщина ее равна ![]() ,
а плотность материала, из которого она изготовлена равна
,
а плотность материала, из которого она изготовлена равна ![]() .
.
Решение
![]() Кинетическая энергия материальной точки,
вращающейся около неподвижной оси, равна
Кинетическая энергия материальной точки,
вращающейся около неподвижной оси, равна ![]() ,
где
,
где ![]() –
угловая скорость, а
–
угловая скорость, а ![]() –
момент инерции относительно оси вращения, причем
–
момент инерции относительно оси вращения, причем ![]() (
(![]() –
расстояние от точки до оси вращения,
–
расстояние от точки до оси вращения, ![]() –
масса точки). В данной задаче применить эту формулу ко всей пластинке не
представляется возможным, т.к. каждая точка пластинки расположена на разном
расстоянии от оси вращения и, соответственно, имеет разную кинетическую
энергию.
–
масса точки). В данной задаче применить эту формулу ко всей пластинке не
представляется возможным, т.к. каждая точка пластинки расположена на разном
расстоянии от оси вращения и, соответственно, имеет разную кинетическую
энергию.
Рассмотрим сечение данной пластины.
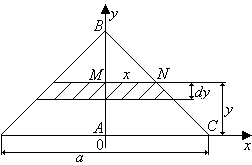 Систему координат расположим так, как
показано на рисунке (пластина вращается около оси Ох). Выделим элементарный
слой в пластине. Обозначим его толщину
Систему координат расположим так, как
показано на рисунке (пластина вращается около оси Ох). Выделим элементарный
слой в пластине. Обозначим его толщину ![]() .
Считаем толщину этого слоя настолько малой, что все его точки находятся на
расстоянии
.
Считаем толщину этого слоя настолько малой, что все его точки находятся на
расстоянии ![]() от
оси Ох. Так как все точки слоя находятся на одинаковом расстоянии от оси
вращения (ось Ох), то они имеют равную кинетическую энергию.
от
оси Ох. Так как все точки слоя находятся на одинаковом расстоянии от оси
вращения (ось Ох), то они имеют равную кинетическую энергию.
Найдем момент инерции ![]() выделенного
слоя.
выделенного
слоя. ![]()
![]() ,
где
,
где ![]() –
масса слоя. С другой стороны,
–
масса слоя. С другой стороны, ![]() ,
где
,
где ![]() –
объем слоя. Учитывая то, что толщина выделенного элемента сколь угодно мала,
заменим объем выделенного элемента на объем прямоугольного параллелепипеда со
сторонами основания
–
объем слоя. Учитывая то, что толщина выделенного элемента сколь угодно мала,
заменим объем выделенного элемента на объем прямоугольного параллелепипеда со
сторонами основания ![]() и
и
![]() ,
высотой
,
высотой ![]() .
Тогда
.
Тогда ![]() .
Так как
.
Так как ![]() и
и
![]() подобны,
то длины их соответствующих сторон пропорциональны, т.е.
подобны,
то длины их соответствующих сторон пропорциональны, т.е. ![]() .
Далее, т.к.
.
Далее, т.к. ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
то
,
то ![]() .
Подставляя полученное значение в формулу для
.
Подставляя полученное значение в формулу для ![]() ,
получим
,
получим ![]() .
Учитывая
.
Учитывая ![]() ,
,
![]() и
и
![]() ,
логически получаем
,
логически получаем ![]() .
Кинетическая энергия элементарного слоя будет равна
.
Кинетическая энергия элементарного слоя будет равна ![]() .
Так как
.
Так как ![]() ,
то
,
то
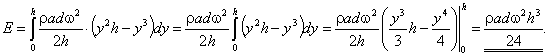
№3
Два электрических заряда: ![]() и
и
![]() находятся
на расстоянии 10 см друг от друга. Разделяющей их средой служит воздух. Сначала
оба заряда закреплены неподвижно, затем заряд q2
освобождается. Тогда под действием силы отталкивания заряд q2
начнет перемещаться, удаляясь от заряда q1. Какую работу
совершит сила отталкивания, когда заряд:
находятся
на расстоянии 10 см друг от друга. Разделяющей их средой служит воздух. Сначала
оба заряда закреплены неподвижно, затем заряд q2
освобождается. Тогда под действием силы отталкивания заряд q2
начнет перемещаться, удаляясь от заряда q1. Какую работу
совершит сила отталкивания, когда заряд:
а) удалится на расстояние 30 см; б) удалится в бесконечность?
Решение
По закону Кулона сила взаимодействия двух электрических зарядов равна ![]() ,
где q1 и q2 – величины зарядов в кулонах, r
– расстояние между зарядами в метрах, электрическая постоянная
,
где q1 и q2 – величины зарядов в кулонах, r
– расстояние между зарядами в метрах, электрическая постоянная ![]() (
(![]() )
и ε – диэлектрическая проницаемость среды относительно вакуума (для
воздуха
)
и ε – диэлектрическая проницаемость среды относительно вакуума (для
воздуха ![]() ).
Однако в нашей задаче расстояние r не является постоянным, оно меняется с
передвижением заряда q2 по оси Ох.
).
Однако в нашей задаче расстояние r не является постоянным, оно меняется с
передвижением заряда q2 по оси Ох.
![]()
Рассмотрим элементарный отрезок ![]() ,
полагая его настолько малым, что сила взаимодействия зарядов на нем практически
не меняется, т.е. остается постоянной.
,
полагая его настолько малым, что сила взаимодействия зарядов на нем практически
не меняется, т.е. остается постоянной.
Согласно закону Кулона, сила взаимодействия зарядов будет равна ![]() .
Чтобы переместить один заряд на расстояние
.
Чтобы переместить один заряд на расстояние ![]() этой
силе придется совершить работу
этой
силе придется совершить работу ![]() Когда
расстояние между зарядами будет 30 см, заряд
Когда
расстояние между зарядами будет 30 см, заряд ![]() пройдет
расстояние
пройдет
расстояние ![]() .Тогда
.Тогда
![]() и
и
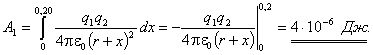
Если заряд удаляется в бесконечность, то
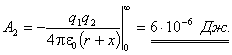
№4
Пластина, имеющая форму эллипса, наполовину погружена в жидкость
(вертикально) так, что одна из осей (длиной 2b) лежит на поверхности.
Как велика сила давления жидкости на каждую из сторон пластинки, если длина
погруженной полуоси эллипса равна а, а плотность жидкости ![]() ?
?
РРРРешение
Как известно, давление жидкости на горизонатльную площадку определяется
по закону Паскаля: ![]() ,
где
,
где ![]() –
плотность жидкости,
–
плотность жидкости, ![]() –
глубина погружения,
–
глубина погружения, ![]() –
площадь площадки. К пластине, данной в задаче, эта формула неприменима, т.к.
все точки пластины лежат на разной глубине, и, соответственно, испытавают
разное давление.
–
площадь площадки. К пластине, данной в задаче, эта формула неприменима, т.к.
все точки пластины лежат на разной глубине, и, соответственно, испытавают
разное давление.
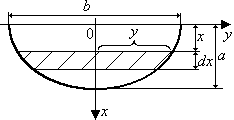 Выделим на пластине элементарную площадку.
Высота этой площадки
Выделим на пластине элементарную площадку.
Высота этой площадки ![]() настолько
мала, что все точки, лежащие на площадке, испытывают практически одинаковое
давление, т.е. на выделенном элементе давление не меняется.
настолько
мала, что все точки, лежащие на площадке, испытывают практически одинаковое
давление, т.е. на выделенном элементе давление не меняется.
![]() .
.
Так как ![]() бесконечно
мало, то площадь выделенной площадки
бесконечно
мало, то площадь выделенной площадки ![]() примерно
будет равна площади прямоугольника со сторонами
примерно
будет равна площади прямоугольника со сторонами ![]() и
и
![]() ,
т.е.
,
т.е. ![]() .
Тогда
.
Тогда ![]() .
.
В данной системе координат эллипс, по форме которого сделана пластинка,
имеет уравнение ![]() ,
где
,
где ![]() .
Отсюда следует
.
Отсюда следует ![]() .
Учитывая
.
Учитывая ![]() и
и
![]() ,
получим
,
получим ![]() ,
где
,
где ![]() .
Тогда давление
.
Тогда давление ![]() на
всю пластину составит:
на
всю пластину составит:
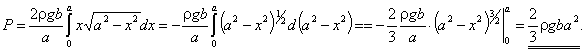
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.