Кинематика: Конспект лекций по курсу "Теоретическая механика" (Векторный способ задания движения. Ускорение. Поступательное движение)

свою очередь его положение в системе координат XYZлегко определить тремя углами.

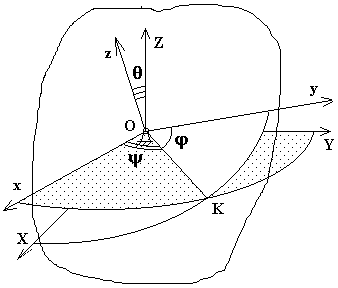
Рис. 14

Следуя Эйлеру, эти углы определяются следующим образом. Выбирается дополнительная подвижная система координат , жестко связанная с телом. Пусть отрезок ОК будет линией пересечения плоскостей XOY и xOy. Эйлер ввел следующие углы, определяющие положение подвижной системы координат относительно неподвижной:

угол СОБСТВЕННОГО ВРАЩЕНИЯ;

угол ПРЕЦЕССИИ;

угол НУТАЦИИ.

Таким образом, ЗАКОНОМ ДВИЖЕНИЯ ТЕЛА С ОДНОЙ ЗАКРЕПЛЕННОЙ ТОЧКОЙ ЯВЛЯЮТСЯ ТРИ ЗАВИСИМОСТИ УГЛОВ ПОВОРОТА.

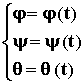
Первые и вторые производные от этих зависимостей будут соответствующими угловыми скоростями и угловыми ускорениями тела.

В плоских задачах это не имело значения, но при решении пространственных важно знать, что УГОЛ ПОВОРОТА, УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ ЯВЛЯЮТСЯ ВЕКТОРАМИ, которые располагаются ВСЕГДА НА ОСИ ВРАЩЕНИЯ. Причем вектор угла поворота и вектор угловой скорости направлены в ту сторону, откуда вращение тела видно против часовой стрелки, а угловое ускорение совпадает с направлением угловой скорости, если тело ускоряется и противоположно ему, если движение замедляется.

Эйлеровы углы в каждый момент времени определяют вектор действительного вращения тела, так называемую МГНОВЕННУЮ ОСЬ ВРАЩЕНИЯ.

ДВИЖЕНИЕ ТЕЛА С ОДНОЙ ЗАКРЕПЛЕННОЙ ТОЧКОЙ МОЖНО ПОНИМАТЬ КАК ЧИСТОЕ ВРАЩЕНИЕ ВОКРУГ МГНОВЕННОЙ ОСИ.

СВОБОДНОЕ ДВИЖЕНИЕ ТЕЛА

Если на тело не наложены связи – оно находится в СВОБОДНОМ движении. Положение тела в этом случае определяется так: выбирается полюс А, чье положение определяется тремя координатами X_A, Y_A, Z_A, и выбираются эйлеровы углы вращения тела вокруг полюса . Таким образом ЗАКОНОМ СВОБОДНОГО ДВИЖЕНИЯ ТЕЛА ЯВЛЯЮТСЯ ШЕСТЬ ЗАВИСИМОСТЕЙ

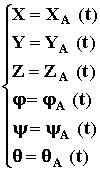
СВОБОДНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА МОЖНО ПОНИМАТЬ КАК ОДНОВРЕМЕННО ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛА ВМЕСТЕ С ПОЛЮСОМ И МГНОВЕННОВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛА ВОКРУГ ПОЛЮСА.

Отметим, что ДВИЖЕНИЕ ПЛОСКОГО ТЕЛА В СВОЕЙ ПЛОСКОСТИ МОЖЕТ БЫТЬ ТОЛЬКО ПОСТУПАТЕЛЬНЫМ, ВРАЩАТЕЛЬНЫМ ИЛИ их комбинацией, т.е. ПЛОСКИМ движением.

СЛОЖНОЕ ДВИЖЕНИЕ ТЕЛ

До сих пор при изложении кинематики не принимался в рассмотрение один очень важный вопрос, а именно: как влияет на характеристики движения тела движение самой системы отсчета?

Вопрос актуальный, так как в нашем распоряжении (в земных условиях) нет практически систем координат неподвижных или движущихся с постоянной скоростью (земная поверхность участвует во вращении нашей планеты вокруг собственной оси, сама планета движется вокруг Солнца и т. д.). Поэтому важно выяснить степень влияния движения самой системы отсчета, чтобы при необходимости вносить поправку в расчеты.

Движение тела называется СЛОЖНЫМ, если оно регистрируется в подвижной системе координат. При этом движение тела относительно системы координат называется ОТНОСИТЕЛЬНЫМ, а движение самой системы координат – ПЕРЕНОСНЫМ.

Рассмотрим движение точки в подвижной системе координат (рис. 15). За малый промежуток времени  точка переместится из положения А в положение В, но одновременно с этим ведь перемещалась и система координат. Следовательно фактически точка окажется в положении С, т. е.

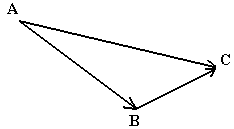
Рис. 15

Поскольку речь идет о малых перемещениях за малые промежутки времени, с незначительной погрешностью можно считать, что  соответствует вектору абсолютной скорости ,  скорости относительного движения ,  скорости переносного движения , т. е.

                                                                       (9)

Теорема Кориолиса

Если продифференцировать равенство (9), то учитывая, что относительная скорость изменяется при изменении переносной и наоборот, в правой части получится не два слагаемых, а четыре

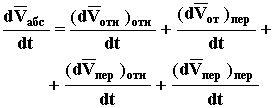
Первое слагаемое в правой части - это собственно относительное ускорение, четвертое - переносное ускорение, а второе и третье - результат взаимного влияния переносного и относительного движения друг на друга. Опуская здесь строгое доказательство, которое впервые получил Кориолис, приводим окончательный результат

где  кориолисово ускорение, равное удвоенному векторному произведению угловой скорости переносного движения на линейную скорость относительного.

ТЕОРЕМА К3. Абсолютное ускорение точки, участвующей в сложном движении, равняется векторной сумме относительного, переносного и кориолисова ускорений.

Доказательство. Без доказательства.

По свойствам векторного произведения  располагается так, чтобы быть перпендикулярным и , и , и направлено в ту сторону, откуда кратчайший поворот от  к  виден против часовой стрелки. Напомним здесь, что вектор угловой скорости всегда лежит на оси вращения. При определении направления кориолисова ускорения можно руководствоваться следующим правилом (правило Жуковского): чтобы получить направление кориолисова ускорения надо вектор относительной скорости спроектировать на плоскость, перпендикулярную оси переносного вращения и затем повернуть эту проекцию на 90 градусов по направлению действительного переносного вращения.

Величина кориолисова ускорения может быть вычислена по формуле

где  острый угол между векторами  и .

Кориолисово ускорение будет отсутствовать (), если

1)  это значит, что система координат движется поступательно или покоится;

2)  это значит, что тело покоится в выбранной системе координат