Преобразователи частоты и параметрические усилители. Теория преобразования на невзаимном электронном приборе

Параметр С=0,5С называется преобразующей емкостью; -преобразующей проводимостью или крутизной преобразования.

Введем обозначения для комплексных параметров преобразования:

                      (4.38)

С учетом этих обозначений (4.36) и (4.37) примут вид

                                    (4.39)

                (4.40)

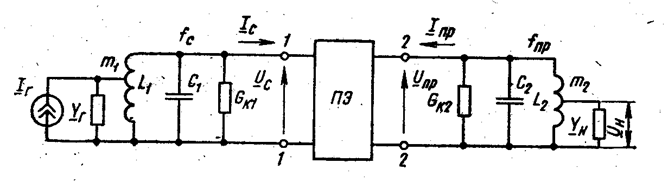
Это уравнения прямого и обратного преобразований соответственно для неинвертирующего (4.39) и инвертирующего (4.40) диодного ПЧ. По форме они совпадают с (4.26), (4.27) и (3.1). Согласно (4.39) и (4.40) ПЭ можно представить в виде линейного четырехполюсника с Y - параметрами (4.38). Общая эквивалентная схема ПЧ с источником сигнала и нагрузкой приведена на рисунке 4.28.

Уравнения источника сигнала с входным контуром и нагрузки с учетом знака определяются выражениями

                                                 (4.41)

Iи                  Yи

(4.42)

Рисунок 4.28

где  — суммарная проводимость входного контураи источникасигнала, пересчитанная к контуру в точках 1-1; —собственная  проводимость входного контура; — проводимость эквивалентной нагрузки ПЭ в точках 2—2; —собственная проводимость выходного контура. В (4.41)  в соответствии с теоремой об эквивалентном генераторе; Е_И—ЭДС источника сигнала.

Найдем коэффициент передачи напряжения ПЭ . Для этого подставим в первое выражение (4.39) уравнение нагрузки (4.42):

-                                                     (4.43)

Отсюда для неинвертирующего ПЧ  

                    (4.44)

Здесь -эквивалентная проводимость выходного контура. Аналогично для инвертирующего ПЧ

                                          (4.45)

Используя вторые уравнения (4.39) и (4.40), можно определить входную проводимость ПЭ в точках 1—1 (см. рисунок 4.28). С учетом (4.44) и (4.45) для неинвертирующего ПЧ

,             (4.46)

для инвертирующего ПЧ

.                                                       (4.47)

Выходную проводимость ПЭ в точках  2—2  найдем из первого уравнения (4.39):

.                                         (4.48)

Здесь  — коэффициент передачи ПЭ при обратном преобразовании. Для его определения подставим во второе выражение (4.39) уравнение (4.41):

или, иначе,

                                                                    (4.49)

где —эквивалентная проводимость входного контура. При рассмотрении обратного преобразования полагаем , поэтому из (4.49) 

.                                                                  (4.50)

Подставляя (4.50) в (4.48), получаем для неинвертирующего ПЧ

.                                                                        (4.51)

Аналогично из (4.40) для инвертирующего ПЧ

.                                                                        (4.52)

Общий или сквозной коэффициент передачи напряжения диодного ПЧ      (см. рисунок 4.28) найдем как , где . Для определения решим систему уравнений (4.39) или (4.40) с учетом (4.41) и (4.42). Воспользуемся выражениями (4.43) и (4.49):

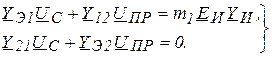                                                       (4.53)

На основании формулы Крамера найдем , где определитель системы (4.53); —определитель, получающийся из  заменой второго столбца правой частью (4.53), т. е. свободными членами:

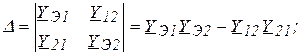
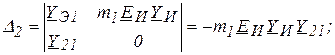
Отсюда .

Общий коэффициент передачи напряжения

       .       (4.54)

Это общее выражение позволяет рассчитать АЧХ и ФЧХ диодного ПЧ.

Диод ПЧ используется в одном из следующих режимов:

напряжение гетеродина изменяется преимущественно в области прямого тока. В ПЧ применяется диод с малой емкостью. В этом случае главную роль играет нелинейная резистивность диода. Такой ПЧ называется  резистивным;

используется закрытый переход диода. В ПЧ применяется диод со сравнительно большой нелинейной емкостью, т. е. варикап. При этом резистивность проявляется слабо. Такой ПЧ называется емкостным.

4.8. Резистивный диодный преобразователь

Применим общую теорию к случаю резистивного ПЧ. Пренебрегая емкостями, из (4.38) получаем параметры,. Подставим их в (4.54) и найдем модуль резонансного коэффициента передачи напряжения:

 ,                                    (4.55)

где; —эквивалентные резонансные проводимости соответственно входного и выходного контуров.

Из (4.55) видно, что  двояко зависит от и , поэтому есть оптимальные значения этих коэффициентов, при которых будет максимум . Исследуем  на экстремум в упрощенном случае, когда можно пренебречь собственными резонансными проводимостями контуров  и , что соответствует действительности. В этом случае

.

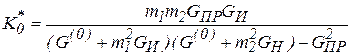Обозначив  и , приведем это выражение к виду

.

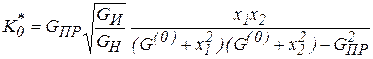Поскольку одинаково зависит от  и , максимум  имеет место при , поэтому

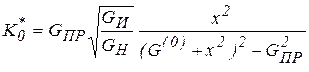 .                                 (4.56)

Решая уравнение , находим , следовательно, ; .

Величина  называется характеристической проводимостью диодного ПЧ. Она играет ту же роль, что и характеристическая проводимость обычного линейного четырехполюсника .

При оптимальных и  из (4.56) следует

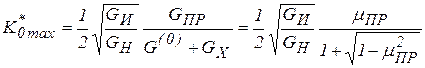,                         (4.57)

где .

Коэффициентом передачи мощности назовем отношение мощности, выделяемой в нагрузке , к номинальной мощности источника сигнала :

.                     (4.58)

С учетом (4.57) из (4.58) получим

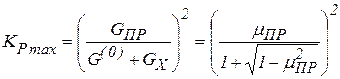.                                           (4.59)

При экспоненциальной аппроксимации ВАХ диода в рабочей   области .

Реально у современных резистивных диодных ПЧ . Для сравнения у современных транзисторных СВЧ смесителей значение  практически совпадает с  в усилительном режиме и составляет 8... 10 дБ, а иногда и более. По уровню интермодуляционных искажений третьего порядка диодные