Расчет плоскостной импедансной антенны (направитель - гребенчатый, длина волны - 32 мм), страница 2

Расчёты по (4) и (7) показывают , что уменьшение фазовой скорости, начиная от v=c, сопровождается постепенным сужением основного лепестка ДН(это ведёт к увеличению КНД) и ростом боковых лепестков, что ведёт к уменьшению КНД. Излучение в главном направлении сначала растёт, достигая максимума при некоторой оптимальной (для данного значения L=nd)  величине c/v, а затем уменьшается и обращается в нуль при некоторой критической величине (c/v)_кр=1+λ/L.

Следовательно, при оптимальной величине (c/v) КНД достигает максимального значения.

КНД антенны с осевым излучением (в случае ненаправленной антенны ) можно рассчитать по формуле

(8)

  

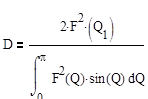
заменив в ней F(Q) выражением (7). При этом

(9)

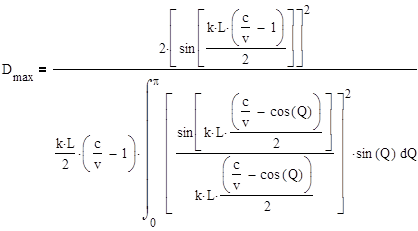
Таким образом, КНД является функцией результирующего сдвига фаз ψ_n между полями, создаваемыми крайними элементами антенны в точке, лежащей на продолжении оси антенны. Следовательно, приближенным условием получения максимального КНД является

(10)  ψ_{n опт}=kL(c/v-1)=π.

Воспользовавшись формулой(10), можно определить оптимальную величину c/v при заданной длине антенны   L/λ.

(11)  (c/v)_опт=1+λ/2L

(12)  (L/λ.)_опт=1/(2(c/v-1))

Как видно из (12), оптимальная длина антенны увеличивается с увеличением фазовой скорости. Данные соотношения справедливы только при направленных или слабонаправленных элементах антенны. При выполнении условия (11) КНД

(13)  D_max=(7-8)(L/λ)_опт

На рис.5 приведены графики зависимости D/(L/λ) от величины (c/v) для антенн различной длины. Максимумы кривых соответствуют значению Ψ_n=180˚.Из графиков видно, что при переходе от режима наклонного к режиму осевого излучения КНД резко возрастает.

Рис.5.

          D(λ/L)

                                L₂/λ=10                      L₁/λ=1

     8

     6

                                                    

     4                                                        

2

Область наклонного

Излучения                                                А                  В

 

0.2     0.4    0.6    0.8     1     1.2     1.4    1.6    1.8                   c/v

             Поперечное излучение                         L₂/λ

                       

                                                                               L₁/λ 

                Области осевого излучения

В точке А  (c/v)_опт=1+λ/2L₂;

В точке В  (c/v)_опт=1+λ/2L_1.

Ширина ДН (2Q₀) антенны, работающей в оптимальном режиме на основании формулы (7)( полагая F₁(Q)=1) находится из условия kL(c/v-cosQ₀)/2=π.

Подставляя вместо c/v выражение (11) и проводя рассуждения, аналогичные случаю c/v=1, получаем sinQ₀=√λ/L или при малых λ/L.

(14)  2Q₀≈2√λ/L

Как видно из сравнения (6) и(14), оптимальная АБВ имеет ДН в √2 раз уже, чем антенна той же длинны c/v=1.

Ширина ДН по половинной мощности при λ/L<<1

(15)  2Q_0.5≈61˚√λ/L.

Максимальная величина нормированной характеристики направленности оптимальной антенны, определяемая по (7) при Q=0 и c/v=1+λ/2L, равна 2/π. Положив в (7) аргумент синуса равным 3π/2, найдём cosQ_max1.Подставляя в (7) полученное значение cosQ_max1 и заменяя c/v выражением (11), получаем F(Q_max1)=2π/3. Относительный уровень первого бокового лепестка

(16)  ξ₁=F(Q_max1)/F(Q=0)=1/3≈33%.

Если длина антенны L>L_опт, то излучение в главном направлении уменьшается, и растут боковые лепестки. При L=2L_опт излучение при Q=0 прекращается. При L< L_опт главный лепесток ДН расширяется , уровень боковых лепестков уменьшается.

В антеннах бегущей волны, применяющихся а практике, амплитуда возбуждающего тока уменьшается вдоль оси решётки по экспоненциальному закону I₂=I₁e^-ade^-ikdc/v. Это имеет место в следствие потерь энергии в антенне или постепенного излучения энергии элементами антенны. При расчётах в некоторых случаях этим уменьшением пренебрегают.