Разработка устройств цифрового формирования и обработки сигналов системы передачи дискретных сообщений по частотно ограниченным каналам связи (удельная скорость передачи – 2 бит∙с/Гц, разрядность ЦАП – 4, вид модуляции – ФМ)

Сибирский Государственный Университет Телекоммуникаций и информатики

Курсовая работа

по курсу МО ЦОС на тему:

«Разработка устройства цифрового формирования и обработки сигналов системы передачи дискретных сообщений по частотно ограниченным каналам связи»

Выполнил: ст. гр. РА-05

Проверил:

Новосибирск 2003

Содержание

Введение............................................................................................................................. 3

Исходные данные............................................................................................................... 4

Разработка и описание обобщенной структурной схемы цифрового формирователя 5

Выбор длительности и количества элементарных сигналов......................................... 6

Вид элементарного сигнала. Расчет энергии отбрасываемой части............................. 7

Алгоритм вычисления сигнала....................................................................................... 10

Расчет отсчетов сигнала между характеристическими моментами времени............ 11

Расчет спектра сигнала на выходе формирователя...................................................... 12

Расчет мощности шума квантования на выходе формирователя............................... 12

Разработка схемы цифрового формирователя.............................................................. 14

Структурная схема приемника....................................................................................... 15

Заключение....................................................................................................................... 16

Список используемой литературы................................................................................. 17

Введение

Цифровая обработка сигналов – научное направление, связанное с разработкой и оптимизацией алгоритмов преобразования цифровых сигналов с учетом особенности среды их реализации.

В наш век тотальной компьютеризации цифровая  техника занимает главенствующее положение во всех (большинстве) сферах нашей жизни. Связь не является исключением.

Исходные данные

Удельная скорость передачи 2

Разрядность ЦАПа = 4

Вид модуляции – ФМ

Разработка и описание обобщенной структурной схемы цифрового формирователя

Модулятор

ЦФ

АЦП

ФНЧ

ИС

помехи

Линия связи

СУ

ПФ

ЦАП

ПУ

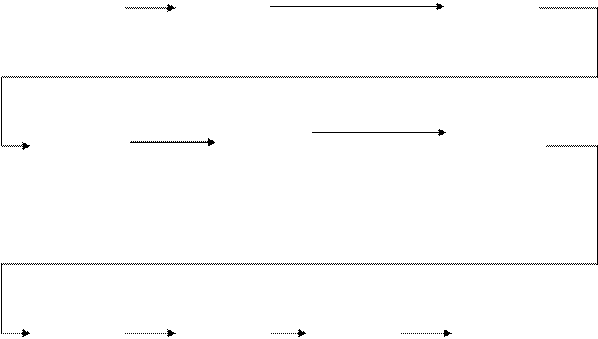
ИС – источник сообщения

ФНЧ – фильтр низкой частоты

АЦП – Аналого-цифровой преобразователь

ЦФ – Цифровой фильтр

ПУ - Помехоустойчивое устройство

ЦАП – Цифро-аналоговый преобразователь

ПФ – Полосовой фильтр

СУ – Согласующее устройство

Выбор длительности и количества элементарных сигналов

В реальные каналы связи для передачи сигналов по частотно ограниченному каналу используется сигнал вида , но он бесконечен во времени, поэтому его сглаживают по косинусоидальному закону. К тому же такой сигнал будет иметь спектр, удовлетворяющий условию Найквиста и обладает условием селективности.

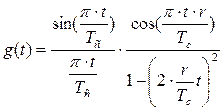 , где

r – коэффициент сглаживания.

, т.к. 0 < r < 1 то

N = 4 – количество элементарных сигналов

Где N – число элементарных сигналов,

 - Удельная скорость передачи информации

r – коэффициент сглаживания

F – частота сигнала

Рассчитаем полосу пропускания канала связи по формуле:

f₁=r*F+F=1*F+F=2*F

Ширина спектра: f₁ = 2 F

Зная заданные и полученные значения можно рассчитать длительность элементарного сигнала по формуле:

Вид элементарного сигнала. Расчет энергии отбрасываемой части

Прежде всего, для расчета вида элементарного сигнала необходимо рассчитать интервал дискретизации:

, где f_д – частота дискретизации.

Частота дискретизации выбирается с учетом того, что в спектре должна оставаться полоса расфильтровки ∆f: ее условие:

∆f = f_д – 2 f₁

Выберем частоту дискретизации f_д = 8 F, тогда

Количество отчетов на одном T_c будет определяться формулой:

Проверить условие для полосы расфильтровки

∆f = f_д – 2 f₁ = 8 F – 2* 2 F = 4 F

Расчет отчетов элементарного сигнала производится по формуле:

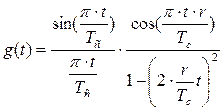
Количество элементарных сигналов равно 4. Пусть два из них будут иметь максимумы +3 и –3, а два других +1 и –1.

Данный сигнал симметричен относительно 0, следовательно рассчитаем отсчеты справа от 0. Расчет сведем в таблицу:

t/Tc	0	1/4	2/4	3/4	1	5/4	6/4	7/4	2	9/4	10/4	11/4	3
g(t)	1	0,85	-	0,17	0	-0,024	0	8,08·10-3	0	-3,68·10-3	0	1,9·10-3	0
g(t)	-1	-0,85	-	-0,17	0	0,024	0	-8,08·10-3	0	3,68·10-3	0	-1,9·10-3	0
g(t)	3	2,55	-	0,51	0	-0,07	0	0,024	0	-0,011	0	5,94·10-3	0
g(t)	-3	-2,55	-	-0,51	0	0,07	0	-0,024	0	0,011	0	-5,94·10-3	0

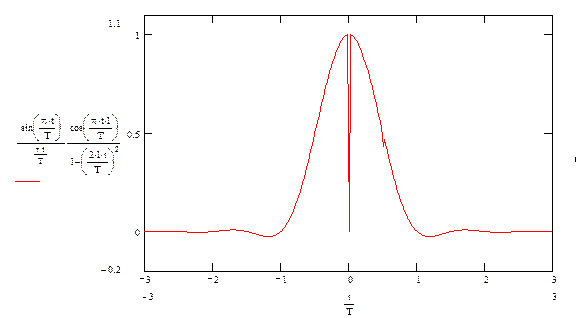
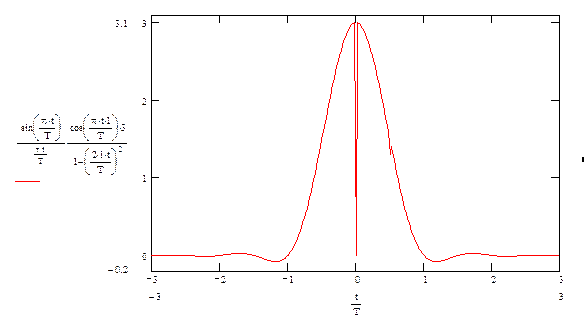
Сигналы с максимумами –3 и –1 будут иметь аналогичный вид, только с противоположной фазой.

Рассчитанные элементарные сигналы являются бесконечными во времени, что является неприемлемым. Но они быстро затухают по амплитуде, поэтому при передаче можно отбросить некоторую часть сигнала. При этом необходимо учитывать тот факт, что энергия отбрасываемой части не должна превышать 10 % энергии всего сигнала.

Как видно из расчетов сигналов: 9, 10, 11, 12 – й отсчеты имеют малые значения.

Рассчитаем энергию отбрасываемой  части в процентах. Для этого рассчитаем энергию всего сигнала и отбрасываемой части.

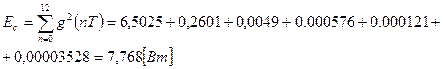
Рассчитаем энергию отбрасываемой части:

Найдем процентное соотношение энергий элементарного сигнала и отбрасываемой части.

Таким образом энергия отбрасываемой части много меньше 10 % полной энергии сигнала.

Алгоритм вычисления сигнала

Расчет отсчетов сигнала между характеристическими моментами времени

Приведем пример расчета отсчетов выходного сигнала.

Пусть нам требуется передать двоичную последовательность 00101101. Количество информации, переносимое элементарным сигналом, определяется выражением:

, где N – число элементарных сигналов

N = 4 следовательно каждый сигнал несет 2 Бит.

Разобьем данную последовательность на 4 пары: 00, 01, 10, 11.

Пусть последовательность 00 будет передаваться сигналом с амплитудой +3, 10 - -3, 01 - -1, 11 - +1.

Графически формирование выходного сигнала изображена на рисунке ниже