Измерение и определение характеристик по топографической карте масштаба 1:25000

Определить среднюю высоту поверхности   точечным способом в пределах четырехугольника при расстоянии между узлами квадратной сетки ∆l, равными 1 см в масштабе карты.

Рассчитать расстояние между узлами квадратной сетки ∆, для определения средней высоты четырехугольника  со средней квадратической ошибкой .

3.  Составить карту перемещения грунта в изолиниях с показом высоты снимаемого и отсыпаемого грунта для планировки заданного участка ( четырехугольника) на уровне его средней высоты (.

Подсчитать объемы перемещаемого грунта: общий , снимаемый , и досыпаемой

Материал для работы :

1.  Топографическая карта масштаба 1: 25 000.

2.   Условные знаки для топографического карт масштабов 1: 25 000, 1: 50 000, 1: 100 000 [20].

Ход задания.

Выполнение первой части задания.

1.  Определить географические координаты (λ,φ) , прямоугольные координаты (x.y) и высоту H каждой из точек четырехугольника. Полученные данные занесены в таблицу 1.

Точки	Географические координаты		Прямоугольные координаты		Высоты H, м
	λ, ° ' "	φ, ° ' "	х , км	У , км
А	65°  47' 10"	53° 42' 16"	5956,300	11683,800	155
Б	65° 47' 30"	53° 43' 10"	5958,275	11684,150	160
С	65° 48' 45"	53° 43' 70"	5959,175	11685,625	165
Д	65° 49' 20"	53° 43' 00"	5958,000	11686,125	147,5

2.  Вычислить площадь четырехугольника АВСД по формуле:

S=

S=  (11684,150-11683,800)+(11686,125-11685,625) +*0,35+5958,725+1,475 +5957,7375*0,5 +5957,15 * (-2,325)= 2085,050625+8789,119375+2978,86875-13850,3737= 2,665005 = 2,5

3.  Вычислить горизонтальное проложение ( l) по формуле:

l=

= = = 2005,8 м

= = = 1727,9 м

= = = 1277,0 м

l= = 2880,2 м

4.  Вычислить  уклон линии   (i)  и угол наклона ( v) соотвественно по формулам:

i=; .

0.0025

= = 0.0029

= 0.0036

5.  Вычисление наклонной длины (L)

Наклонную длину линии L вычислить по формуле:

L=

Вычисление поправок следует провести по формулам:

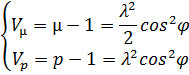
Получаем общие значения:

Вычисление по формулам характеристики, занесены в таблицу .

Линия	Горизонтальное проложение l,м	Уклон линии i	Наклон линии v, ° ' "	Наклонная линия L
АВ	2000.8	0.0025	0°8 '30 "	2007.81
ВС	1727.9	0.0029	0°9 '57 "	1727.907
СД	1277.0	0.0014	0°4 ' 43"	1277.001
ДА	2880.2	0.0036	0°12 '27 "	2880.22

Вычисление периметра (П).

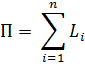
П = 1132.01+1410.86+973.8+2050=5766.9 м

Вычислим поправки :

Частные масштабы длин  и площадей  с точностью до членов первого порядка малости определяются как:

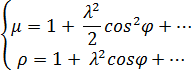
Отклонение от этих величин от единицы используется для характеристики относительного искажения длин  и площадей . Последние с учетом формул вычислим как:

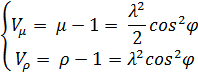
В данных формулах долгота λ и широта определяются для точки, расположенной в центре листа топокарты, причем долготу указанной точки определим относительно осевого меридиана зоны в радианной мере.

Долгота осевого меридиана зоны определяется по формуле:

Для данной карты с номенклатурой У-41-84-Г-в:

Далее определим долготу  для центральной точки листа карты; в данном случае  составит . Тогда:

Полученное значение необходимо перевести в радианную меру:

λ = 0.0401 рад

Широта для центральной точки листа составит 53̊ 42′ 30″

Вычислим искажения длин и площадей :

Поправки за счет искажений проекции в периметр и площадь определим как:

и внесем их в конечный результат:

Вычисление периметра П и площади S четырехугольника:

Периметр четырехугольника АВСД вычисляется по формуле:

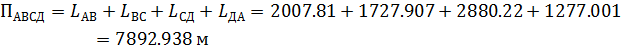
Определим поправки за счет искажений проекции в периметр и площадь:

ΔП = -П*Vμ

ΔS= -S*Vp

ΔП=-7892,938*0,0004=-3,1572 м

ΔS= -2500*0,0008= -2 м

И внесем их в конечный результат:

= 7892,938-3,1572 = 7889,88 м

= 2500-2 = 2498

Результаты вычислений занесены в таблицу 2.

Периметр П, м		Площадь S,	Относительные искажения		Поправки в		Конечные значения
			длин	площадей	Периметр	площадь	Периметр	Площадь
		2500	0,0004	0,0008	-3,1572	-2	7889,88	2498

Выполнение второй части задания.

Вычисление средней высоты.

Первоначально следует построить сетку квадратов (со стороной 1 см), площадь которой полностью накрывала бы изображение четырехугольника, а ориентировка шла по линиям километровой сетки на топокарте (рис. 41).

Вычислить среднюю высоту области  по формуле:

= , в которой Н i – высоты точек, расположенных в узлах квадратной сетки четырехугольника АВСД, n – количество точек, в которых определялись отметки точек.

=

Результаты вычислений отметок следует занести в табл. 13.

Таблица 13. Высоты точек

Номера точек	Высоты точек , м	ΔН=	Δ,
1	163	6,2	38,44
2	157,5	-0,3	0,09
3	156	-0,8	0,64
4	153	-3,8	14,44
5	152	-4,8	23,04
6	149	-6,8	46,24
7	152	-4,8	23,04
8	159,5	2,7	7,29
9	156	-0,8	0,64
10	155,5	-1,3	1,69
11	152,5	-4,3	18,49
12	152	-4,8	23,04
13	162	5,2	27,04
14	163	6,2	38,44
15	162	5,2	27,04
16	152,5	-4,3	18,49
17	150,5	-6,3	39,69
18	150	-6,8	46,24
19	160,5	3,7	13,69
20	159	2,2	4,84
21	157,5	0,7	0,49
22	157	0,2	0,04
23	158	1,2	1,44
24	157,5	0,7	0,49
25	162	5,2	27,04
26	159	2,2	4,84
27	162	5,2	27,04
28	160	3,2	10,24
29	155	-1,8	3,24
30	152	-4,8	23,04
31	161	4,2	17,64
32	160	5,2	27,04
33	159	2,2	4,84
34	156	-0,8	0,64
35	155,5	-1,3	1,69
36	156	-0,8	0,64
37	160	3,2	10,64
38	158,5	1,7	2,89
39	158	1,2	1,44
40	157,5	0,7	0,49
41	156	-0,8	0,64
42	158	1,2	1,44
43	155	-1,8	3,24
44	156	-0,8	0,64
45	155,5	-1,3	1,69
46	157,5	0,7	0,49
47	155	-1,8	3,24

Определение параметров новой (искомой) точечной квадратной сетки

Расчет числа точек выполнить по формуле  , в которой

 = 1 м (по условию задания); (h=5–высота сечения рельефа на топографической карте); . Расстояние между точками квадратной сетки рассчитать по формуле:  и выразить его в масштабе карты. При этом в формуле следует использовать конечное значение площади четырехугольника , найденное ранее в первой части задания.

Результаты вычислений оформим в таблицу

Средняя высота , м	Среднеквадратическое отклонение , м	Количество точек (искомое)	Расстояние между точками на местности , м	Расстояние между точками в масштабе карты ,см
156,8	7,12	53	257,8	1,01

Выполнение третьей части задания

Вычисление объемов перемещаемого грунта осуществим с использованием точечной палетки, по формуле:

,

где i – точки, в которых , и

где i – точки, в которых .

Общий объем перемещаемого грунта вычислим как:

Оценку погрешности определения объемов грунта выполним по формуле:

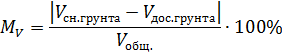
Результаты вычисления характеристик

Объемы грунтов			Относит. Погрешность , %
, м³	, м³	, м³
3108503,55	3106682,2	6215185.75	0,3

Построение фрагмента эскиза карты перемещения грунта

Построение фрагмента выполняем в программе CorelDraw по отсканированному участку карты.

Вычертим контур четырехугольника и изолинии высоты планировки участка, снимаемого и досыпаемого грунтов.

Изолинии проводим через 5 метров интерполированием. За нулевую изолинию перемещения грунта принимаем изолинию, проходящую через точки, соответствующие средней высоте области. Изолинии снимаемого и досыпаемого грунтов строим путем отсчета от «нулевой» изолинии.

Изолинии снимаемого грунта помечаем знаком «минус» у своих цифровых