Расчеты устойчивости подпорной стенки. Расчет устойчивости стенки против сдвига в плоскости подошвы

расстояние от поверхности основания до точки, где определяется пассивное давление;

с₀ – удельное сцепление грунта основания, с₀=35кПа;

λ_р – коэффициент пассивного давления, который вычисляется по формуле (3).

                             (9)

где φ₀ – угол внутреннего трения грунта , φ=28° .

σ_р^'=2·35=116,482кПа.

Найдем вторую составляющую пассивного давления.

При z₁=0 (на поверхности засыпки):   σ_р^''=0.

При z₁=d=1,5м (на уровне подошвы стенки):   σ_р^''= 19,4·1,5·2,769=80,578кПа.

В расчете на единицу длины подпорной стенки результирующие этих давлений вычисляются по площадям своих эпюр:

                                                  (10)

Е_р^'=116,482·1,5=174,723кН.

Е_р^''=0,5·19,4·1,5²·2,769=60,433кН.

Эти силы считают приложенными нормально к контактной грани стенки и проходящими через центры тяжести эпюр, соответственно на расстояниях d/2=1,5/2=0,75м  и  d/3=1,5/3=0,5м от уровня подошвы подпорной стенки (см. рис.2).

2.2. Расчет устойчивости стенки против сдвига в плоскости подошвы

Если активное давление достаточно велико, то оно может сдвинуть подпорную стенку в горизонтальном направлении, так что произойдет сдвиг подошвы стенки по грунту. Такому смещению стенки препятствуют силы пассивного отпора грунта и силы трения подошвы стенки о грунт.  По причине шероховатости подошвы стенки принято считать, что в плоскости подошвы происходит сдвиг грунта по грунту. Поэтому сила трения по подошве определяется в соответствии с законом Кулона по формуле

                            (11)

где G – вес стенки.

Для подсчета веса подпорной стенки ее поперечное сечение удобно разделить на элементарные фигуры: прямоугольники и треугольники, как показано на рис.3. Вес любой такой части на единицу длины стенки определяется произведением

                               (12)

где А_i – площадь соответствующей фигуры.

γ_б – удельный вес материала стенки (бетона), γ_б=23кН/м³.

Найдем площади фигур:

А₁=0,5·d·dtgβ°;  А₁=0,5·1,5·1,5tg19⁰=0,387м².

β=19° из исходных данных;

А₂=0,5h·htg19°;  А₂=0,5·6,2·6,2·0,344=6,618м²;

А₁=0,5·h;  А₁=0,5·6,2=3,1м²;

Вес стенки:

G₁=23·0,387=8,909кН;

G₂=23·6,618=152,226кН;

G₃=23·3,1=71,3кН;

G= G₁+ G₂+ G₃;

G=8,909+152,226+71,3=232,435кН.

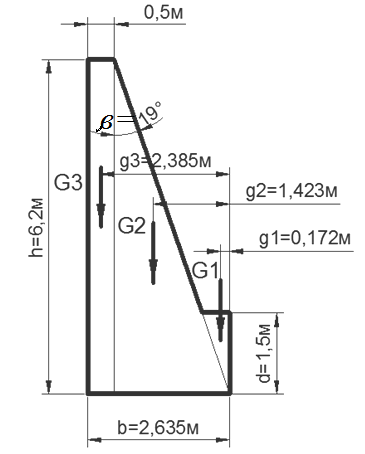
Рисунок 3 – Схема для расчета веса стенки

Тогда сила трения по подошве согласно формуле (11) будет равна:

Т=232,435·tg20^o+35·2,635=176,824кН.

Степень устойчивости стенки против сдвига может быть оценена по коэффициенту запаса устойчивости

Q_z, Q_r – результирующие удерживающих и сдвигающих сил:

             (14)

Q_z=174,723+60,433+17,813+176,824=429,793кН.

 Q_r=122,116кН.

=3,52.

Стенка устойчива против сдвига , если выполняется условие [1]:

где γ_n – коэффициент надежности по назначению сооружения, принимаемый равным 1,1;    m – коэффициент условий работы, принимаемый равным 0,9.

Условие устойчивости стенки против сдвига:

Вывод: Условие выполняется, следовательно стенка устойчива против сдвига.

2.3. Расчет устойчивости стенки против опрокидывания

При достаточно больших высоте подпорной стенки и величине активного давления может произойти опрокидывание стенки относительно переднего ребра фундаментной плиты (точка А₁ на рис. 2). Очевидно, опрокинуть стенку стремятся сила активного давления Е_а", удерживают от опрокидывания силы собственного веса стенки G₁ G₂, G₃, сила активного давления Е_а' и силы пассивного давления Е_р' и Е_р".    

Степень устойчивости стенки против опрокидывания оценивается коэффициентом запаса устойчивости:

                                                    (16)

где M_z, M_u – момент удерживающих и момент опрокидывающих сил:

где - плечи сил  относительно точки А₁.

 

M_z=8,909·0,172+152,226·1,423+71,3·2,238+174,723·0,75+60,433·0,5+17,813·3,1==594,198кНм

                    

M_u=122,116·2,067=252,414кНм.

                                    

Стенка устойчива против опрокидывания, если выполняется условие [1]

                                     где γ_n – коэффициент надежности по назначению сооружения, принимаемый равным 1,1;    m – коэффициент условий работы, принимаемый равным 0,8.

Условие устойчивости стенки против опрокидывания:

Вывод: Условие выполняется, следовательно стенка устойчива против опрокидывания.

2.4. Расчет устойчивости основания стенки против сдвига по круглоцилиндрическим поверхностям скольжения

Помимо потери устойчивости самой подпорной стенки при большой нагрузке может произойти потеря устойчивости ее основания. В практике проектирования широко применяется проверка возможности потери устойчивости основания посредством сдвига по круглоцилиндрической поверхности скольжения. В полном объеме расчет этот трудоемок, поскольку требуется выполнить целый ряд проверок устойчивости по различным поверхностям скольжения, чтобы определить наиболее опасную круглоцилиндрическую поверхность скольжения и соответствующий ей наименьший коэффициент запаса устойчивости [2]. В курсовой работе этот расчет выполняется в сокращенном объеме и до некоторой степени в упрощенном виде: выполняются  проверки по трем поверхностям скольжения с тремя центрами вращения: С₁, С₂, С₃ (рис.4, 6, 7).

Поскольку излагаемый метод расчета относится к графоаналитическим методам, то точность его зависит, в частности, от масштаба и аккуратности выполнения расчетной схемы.

Проверка устойчивости основания на сдвиг по каждой круглоцилиндрической поверхности скольжения выполняется в следующей последовательности.

а) Проверка устойчивости по поверхности скольжения относительно центра вращения С₁.

На расчетной схеме, вычерченной в масштабе 1:100, с помощью циркуля