Анализ данных эксперимента показал, что средняя плотность тока в катодной привязке СВД, стабилизированной однородным АМП, в процессе её развития после поджига в центре катода не может упасть ниже некоторого минимального значения. Это значение не зависит от тока СВД, а определяется индукцией АМП (и длиной дуги). Другими словами, развитие СВД останавливается, когда в следствие расширения привязки плотность тока в ней снизится до некоторого уровня, определяемого индукцией АМП и не зависящего от тока. Эта минимальная для данных значений АМП и длины дуги величина плотности тока и есть та плотность тока, при которой дуга будет гореть стационарно. Поэтому её можно назвать «нормальной» плотностью тока jn. Нормальная плотность тока растёт с ростом индукции АМП и, наоборот, падает при увеличении длины дуги. Теоретической модели этого явления пока не создано. (Существование нормальной плотности тока характерно для различных видов электрического разряда, например, для тлеющего. Однако физика процессов, обуславливающая существование феномена нормальной плотности тока в различных видах разрядов, различна.) На катоде большого размера дуга будет стационарно (квазистационарно) гореть, когда плотность тока упадет до значения j = jn. Режим горения СВД на реальном катоде ограниченного размера будет зависеть от соотношения средней плотности тока J0 = I/S (S – площадь катодной накладки) и jn. Поскольку jn определяется B, то и соотношение между J0 и jn будет определяться значением B. При jn < J0 площадь катодной привязки должна превосходитьплощадь накладки, т.е КП должны частично переместиться на боковую поверхность (участок 1 ВТХ). При jn > J0 площадь привязки должна быть меньше площади накладки (участок 3 ВТХ). Равенство jn = J0 выполняется при некотором фиксированном значении B. То есть, участок 2 должен практически отсутствовать. Наличие более или менее протяжённого участка 2 – результат действия «эффекта края» электрода. При значениях J0, близких к jn, но несколько меньших, КП будут удерживаться на краю поверхности накладки потому, что края, выступы и стыки поверхностей энергетически выгодны для КП. В таких местах теплоотвод по сравнению с плоской поверхностью меньше.
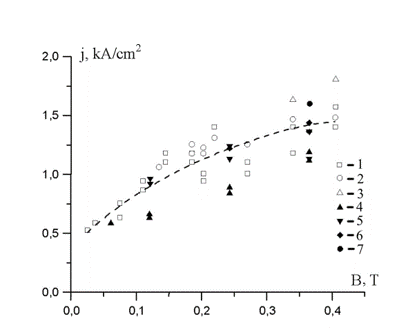
Зависимость нормальной плотности тока в СВД от индукции аксиального магнитного поля. Электроды CuCr; h=6 mm. Пустые символы – электроды диаметром 30 mm. Заполненные символы – электроды диаметром 50 mm. 1. I=3 kA; 2. – 7.5 kA; 3. – 12 kA; 4. – 11.5 kA; 5. – 18 kA; 6. – 24 kA; 7. – 32 kA.
Сильноточная вакуумная дуга.
СВД, стабилизированная однородным АМП. Некоторые выводы для практического использования.
При B1 < B < B2 , т.е. на участке 2 ВТХ, напряжение на СВД, стабилизированной одноролным АМП, минимально. Значит при выполнении этих условий энерговклад в дугу при фиксированном токе минимален.
Зависимость напряжение на участке 2 ВТХ U2 от от средней плотности тока J0 дуги по данным, полученным в многочисленных экспериментах с электродами из CuCr при J0 < 2 кА/см2, хорошо аппроксимируются формулой: U2 = 18,1 + 12,1·J0·h Значение U2 получится в Вольтах, если в формулу подставить значение h в см, а J0 – кА/см2.
Напряжение горения дуги на третьем участке практически равно напряжению горения слаботочной дуги U*. Для дуги, горящей на CuCr контактах, U* удовлетворительно аппроксимируется выражением]: U* = 17 + (7.7√B + 0,47)ln(20h) Ззначение U* получится в Вольтах, если в формулу подставить значение h в см, а B – в Теслах. Анализ Вольт-Тесловых характеристик при различных токах и длинах дуги позволил вывести выражение для B1: B1 = 0,1·h0.3·J0 Значение B1 получится в Теслах, если в формулу подставить значение h в см, а J0 – в кА/см2. Выражение для приближённой оценки B2 можно получить, приравняв напряжение на сильноточной дуге на участке 2 ВТХ U2 и напряжение на слаботочной дуге U*. Действительно, B2 – это значение индукции АМП, при котором происходит переход со второго участка на третий, на котором напряжение на сильноточной дуге U ≈ U*. В общем виде выражение для B2 получается громоздким. Удобнее пользоваться приведённым ниже приближённым выражением, в котором численное значение коэффициента K зависит от длины дуги h: B2 = K·J02·h2 Здесь K ≈ 1,6 при 0,15 < h < 0,25; K ≈ 0,6; при 0,35 < h < 0,45; K ≈ 0,4 при 0,5 < h < 0,7; K ≈ 0,3 при 0,9 < h < 1,1 см. Значение B2 получится в Теслах, если в формулу подставить значение h в см, а J0 – в кА/см2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.