Разряд в вакууме. Ток в вакууме при отсутствии заметных объёмных зарядов. Основное различие газовых разрядов и разрядов в вакууме

РАЗРЯД В ВАКУУМЕ Ток в вакууме при отсутствии заметных объёмных зарядов.

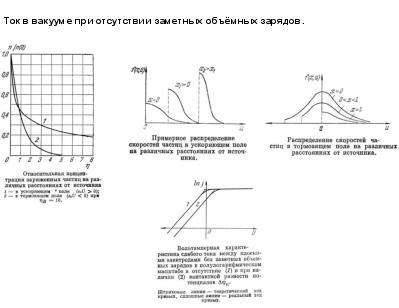
Ток в вакууме при отсутствии заметных объёмных зарядов.

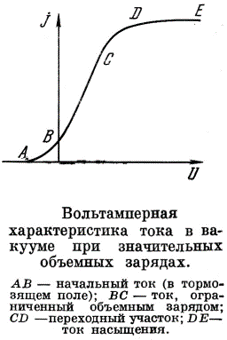
Ток в вакууме при наличии значительных объёмных зарядов. Формула Чайльда-Ленгмюра. (Ускоряющее поле.)

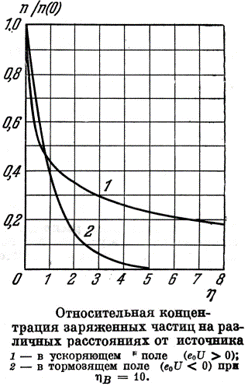
Если плотность потока носителей заряда увеличивается, то увеличивается и их концентрация в промежутке. Соответственно возрастает объёмный заряд и создаваемое им электрическое поле, которое называют самосогласованным, чтобы подчеркнуть двустороннюю связь между ним и движением заряженных носителей.

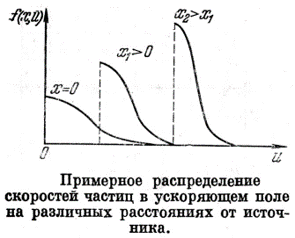
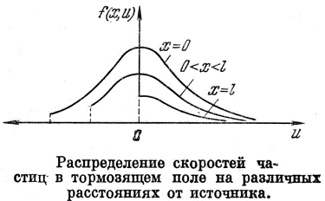
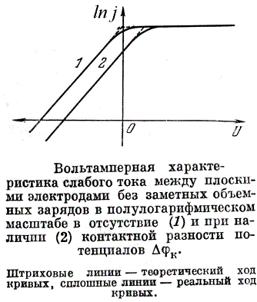
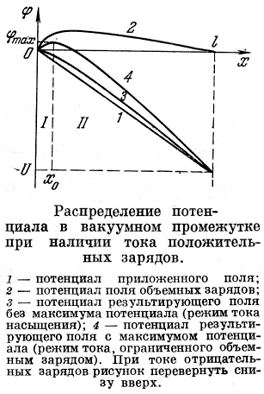
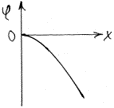
Напряжённость и потенциал результирующего поля: E=E1+E2, φ=φ1+φ2 (начало отсчёта потенциала на эмиттере) E1 и φ1 характеризуют поле поверхностных зарядов на электродах E2 и φ2 – поле объёмных зарядов. 1) Слабый объёмный заряд. Поле всюду направлено к коллектору (кривая 3 на рис.). Все частицы, вылетевшие с эмиттера, достигают коллектора. Режим тока насыщения. 2) Сильный объёмный заряд. На начальном участке φ>0 (обл.I на рис.), дальше φ<0 (обл.II на рис.). При x=x0 φ= φmax. Все носители, прошедшие через максимум потенциала, попадают на коллектор. Фактически, роль эмиттера теперь играет граница областей I и II, расположенная при x=x0 («виртуальный» катод). Поэтому ток на коллектор меньше тока насыщения и определяется φmax. φmax определяется соотношением φ1 и φ2, которое зависит от плотности тока и приложенного напряжения. Точное решение такой задачи достаточно сложное и получается только численными методами. Однако при больших напряжениях x0 и φmax стремятся к нулю и, полагая на поверхности эмиттера dφ/dx=0, можно получить простое аналитическое выражение, связывающее проходящий через промежуток ток с приложенным к нему напряжением («закон трёх вторых» или формулу Чайльда-Ленгмюра). (Ход потенциала вблизи эмиттера для этого случая показан на рис. в нижнем углу слайда)

Если эмитируются электроны, в численном виде:

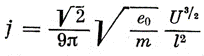
Ход потенциала вблизи эмиттера, когда к коллектору приложено большое напряжение

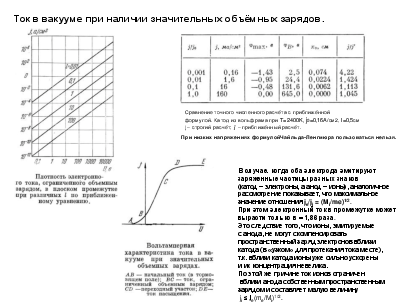
Ток в вакууме при наличии значительных объёмных зарядов.

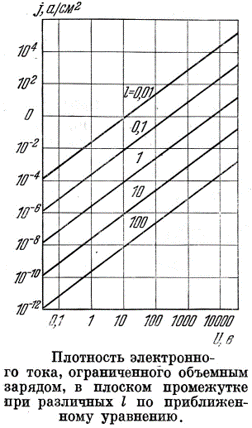
Сравнение точного численного расчёта с приближённой формулой. Катод из вольфрама при T=2400K, j0=0,16A/см2, l=0,5см j – строгий расчёт; j’ – приближённый расчёт.

При низких напряжениях формулойЧайльда-Ленгмюра пользоваться нельзя.

В случае. когда оба электрода эмитируют заряженные частицы разных знаков (катод – электроны, а анод – ионы), аналогичное рассмотрение показывает, что максимальное значение отношения je/ji = (Mi/me)1/2. При этом электронный ток в промежутке может вырасти только в ≈ 1,86 раза. Это следствие того, что ионы, эмитируемые с анода, не могут скомпенсировать пространственный заряд электронов вблизи катода (в «узком» для протекания тока месте), т.к. вблизи катода ионы уже сильно ускорены и их концентрация невелика. По этой же причине ток ионов ограничен вблизи анода собственным пространственным зарядом и составляет малую величину ji ≤ je(me/Mi)1/2.

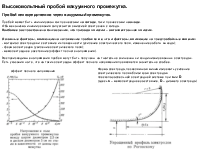
Основное различие газовых разрядов и разрядов в вакууме.

Выше мы видели, что провести ток высокой плотности в вакууме, фактически, невозможно. Для этого нужно приложить нереально высокое напряжение. (На самом деле и очень высокое напряжение не поможет, т.к. в электронном пучке с плотность выше некоторой, называемой критической, развивается неустойчивость и стационарное прохождение тока становится невозможно. Природа неустойчивости электронного пучка с высокой плотностью тока, опять таки, определяется большим объёмным зарядом.) Эмиссия ионов с поверхности анода не может значительно повысить плотность тока. Для прохождения через промежуток тока высокой плотности необходимо иметь в объёме ионы в количестве, достаточном для повсеместной компенсации объёмного заряда электронов. Другими словами, надо иметь квазинейтральную плазму. Поэтому, фактически, дуговые разряды, которые мы будем рассматривать ниже, горящие с высокой плотностью тока при низком напряжении, поджигаются в вакууме, но горят в условиях, когда промежуток заполнен более или менее плотной плазмой. Для горения разрядов с высокой плотностью тока требуется высокая плотность плазмы. Значит такие разряды горят уже не в вакууме, т.к. длины свободного пробега частиц в таких условиях меньше размеров промежутка. Тем не менее, мы различаем газовые и вакуумные дуги и не только потому, что вакуумные разряды поджигаются в вакууме, а потому, что они сами для своего горения должны обеспечить поставку частиц а промежуток. Поставка частиц в промежуток происходит вследствие эрозии электродов. Значит, вакуумная дуга невозможна без эрозии электродов, причём в количестве, необходимом для производства такой концентрации ионов, которая обеспечит компенсацию пространственного заряда электронов во всём промежутке. Горение некоторых видов газовых дуг тоже сопровождается значительной эрозией катода (слаботочные дуги постоянного тока с ненакаливаемым катодом, сильноточные импульсные дуги). Однако и в этих случаях есть принципиальное различие Между газовыми и вакуумными разрядами. Токоперенос в газовых дугах если и происходит в эрозионных парах электродов, то только в прикатодной области. В столбе плазма генерируется из атомов или молекул газа. В вакуумном разряде плазма во всём промежутке должна генерироваться из эрозионных паров. Другого источника плазмообразующего вещества в вакуумных дугах нет. Это накладывает существенные ограничения на режимы, в которых возможно устойчивое горение вакуумных дуг.