таким факторам относится многослойность, неоднородность пласта по толщине, анизотропия пласта, неравномерность размещения скважин, разновременность ввода в разработку отдельных участков залежи и т.д. Поэтому далее будут рассмотрены (постановочно из-за невозможности изложения программ расчетов) основные уравнения и замыкающие соотношения для решения этих уравнений трехмерной одно-, двух- и трехфазных систем в неоднородных пористых средах.
12.6 Теоретические основы численного решения трехмерной однофазной
фильтрации газа в пористой среде
Рассматриваемый случай представляет практический интерес при проектировании разработки газовых месторождений с газовым режимом. При этом учитывается неоднородность пласта, неравномерность размещения скважин, гравитационные силы. Имеются алгоритмы и программы расчетов для линейного и квадратичного законов фильтрации газа в пористой среде. Система нелинейных алгебраических уравнений, получаемая в результате разностной аппроксимации исходного дифференциального уравнения, решается итерационным SIP-методом [40], который представляет собой вариант метода неполной факторизации и характеризуется значительной эффективностью при решении задач фильтрации с резкоменяющимися коэффициентами. Таким образом, для решения поставленной задачи необходимо учесть изменения давления в процессе разработки. Считаются известными состав газа и параметры пласта в отдельных точках залежи, а также начальные распределения давления и температуры по толщине и по площади.
Фильтрация реального газа с учетом сил гравитации при линейном законе записывается в виде:
![]() . (67.12)
. (67.12)
Требуется решение уравнения (67.12) при следующих условиях:
t =0, P(x, y, z, t) = P(x, y, z), (x, y, z)ÎG;
![]() = 0, (x, y, z)ÎГ.
= 0, (x, y, z)ÎГ.
Уравнение (69.12) характеризует отсутствие притока газа (воды) на внешней границе, т.е. ее непроницаемость. Исходя из принятых выше условий, при которых происходит процесс истощения залежи, считаем известными следующие зависимости:
r = r(Р); m = m(Р); m = m(x, y, z, P) и К = К(x, y, z, P), (70.12)
где r — плотность газа; m — коэффициент вязкости; m и К — соответственно коэффициенты пористости и проницаемости пласта в точке с координатами х, у, z; Q — массовая плотность источников (стоков) в этой же точке; G — область газоносности; Г — внешняя граница газоносной площади. Зависимости свойств газа от давления, должны быть установлены экспериментально с учетом состава или же приближенно определены по имеющимся литературным данным. Параметры пласта m и К определяются лабораторным изучением кернового материала, хотя это не всегда возможно (в частности, при вскрытии неустойчивых коллекторов). Кроме того, сохранить истинные значения этих параметров в процессе отбора керна и его последующего изучения не всегда удается. Поэтому в большинстве случаев зависимости m и К от давления принимаются в виде:
m(x, y, z, P) = mн(x, y,
z)×е![]() ; (72.12)
; (72.12)
К(x, y, z, P) = Кн(x, y,
z)×е![]() , (72.12)
, (72.12)
где mн, К н — коэффициенты пористости и проницаемости пласта в точке с координатами х, у, z при начальном пластовом давлении Рн;Рр
am, aк — коэффициенты, учитывающие изменение пористости и проницаемости при изменении давления на 0,1 МПа и определяемые экспериментально. Обычно при прогнозных расчетах используют значения этих коэффициентов, определенных не по кернам данного месторождения, а по данным коэффициентов изменения пористости и проницаемости пород: песчаники, глины, аргалиты, известняки, доломиты и т.д.
Как это было сделано ранее при рассмотрении методических основ численного решения задач фильтрации, приведем уравнения (67.12) к безразмерному виду:
Р* = Р/Р0; r* = r/r0; m* = m/m0; К* = К/К0; х* = х/L0; y* = y/L0;
z* = z/L0; G = r0 L0 g/ Р0; ![]() ;
; ![]() ; (73.12)
; (73.12)
![]() ;
; ![]() , где Р0, r0, m0, L0, К0, m0
— характерные значения этих параметров.
, где Р0, r0, m0, L0, К0, m0
— характерные значения этих параметров.
С учетом (73.12), опуская индексы-звездочки вместо (67.12), получим:
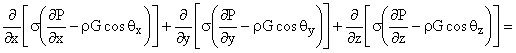
= ![]() , (74.12)
, (74.12)
где ![]() и
и ![]() ; qх, qу, qz — углы между вектором g и осями х,
у, z. Решение уравнения (74.12) при начальном и граничных условиях, выраженных
через (68.12) и (69.12), позволяет прогнозировать изменение давления Р в любой
точке залежи и в любой момент времени в процессе разработки, независимо от
формы залежи, размещения скважин, их дебитов и т.д.
; qх, qу, qz — углы между вектором g и осями х,
у, z. Решение уравнения (74.12) при начальном и граничных условиях, выраженных
через (68.12) и (69.12), позволяет прогнозировать изменение давления Р в любой
точке залежи и в любой момент времени в процессе разработки, независимо от
формы залежи, размещения скважин, их дебитов и т.д.
Решение уравнения (74.12) рассмотрим на примере полосообразной залежи, дренируемой одной несовершенной вертикальной скважиной [см. рис.5.12]. Для конечно-разностной аппроксимации уравнения (74.12) в работе [40] предложена неявная семиточечная разностная схема типа "крест". Аналогично с решением уравнения (62.12) представим уравнение (74.12) в разностной форме для точки с индексами i, j, к:
![]()
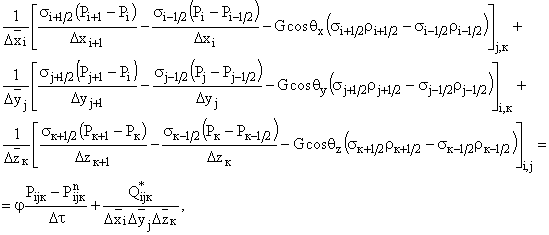 (75.12)
(75.12)
где ![]() —
средние шаги по пространственным переменным; Рn — давление на
временном слое n; Q* — безразмерный массовый дебит узла с сеточными
координатами i, j, к. Если умножить (75.12) на
—
средние шаги по пространственным переменным; Рn — давление на
временном слое n; Q* — безразмерный массовый дебит узла с сеточными
координатами i, j, к. Если умножить (75.12) на ![]() и
сгруппировать коэффициенты при неизвестных давлениях на (n+1) временном слое,
то вместо (75.12) получим:
и
сгруппировать коэффициенты при неизвестных давлениях на (n+1) временном слое,
то вместо (75.12) получим:
![]() . (76.12)
. (76.12)
В уравнении (76.12) опущены индексы i, j, к при коэффициентах А, B, C, D, H, Z и F. Значения этих коэффициентов определяются формулами:
![]() ;
;  ;
; 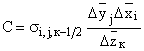 ;
;
![]() ;
; 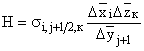 ;
; 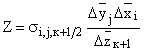 ;
;
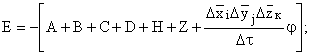
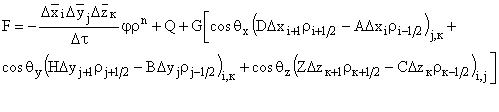 . (77.12)
. (77.12)
В уравнениях системы (77.12) параметры s, j и r относятся к (n+1)-му временному слою. Если записать уравнение (76.12) для всех узлов сеточной области и исключить неизвестные давления на контуре области, а также использовать конечно-разностную аппроксимацию граничного условия (69.12), то получится замкнутая система алгебраических уравнений.
В матричной форме систему (76.12) можно представить в виде:
МР = F. (78.12)
Для произвольного внутреннего узла сетки в разностное уравнение (76.12) входят семь неизвестных, т.е. система является семидиагональной матрицей. В соответствии с алгоритмом SIP-метода прибавляя в (78.12) некоторый вектор NP, получим:
(M + N)P = F + NP. (79.12)
Матрицу N выбирают таким образом [40], чтобы матрицу (M + N) можно было представить в виде произведения двух треугольных матриц L1 и L2. Тогда вместо (79.12) можно записать:
L1 × L2 × Р = F + NP, (80.12)
где L1 и L2 — нижняя и верхняя треугольные матрицы. Решение матричного уравнения (78.12) можно представить на основе следующего итерационного процесса:
L1 × L2 × Рm+1 = F + NPm, (80.12)
где Рm+1 и Pm — векторы давления на m-й и (m+1)-й итерациях
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.