





Кратные, криволинейные и поверхностные интегралы.
Элементы теории поля.
Тесты для самопроверки.
Задание 1. Дайте определение криворлинейного интеграла второго рода (КРИ-II). Запишите формулы для вычисления КРИ-II. К вычислению какого определенного интеграла сводится вычисление криволинейного интеграла
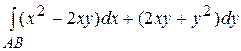 , где АВ
– дуга параболы
, где АВ
– дуга параболы ![]() от
т. А (1, 2) до т. В (2, 8)?
от
т. А (1, 2) до т. В (2, 8)?
Варианты ответов:
А) 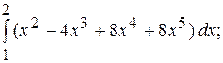 В)
В) 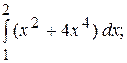
С) 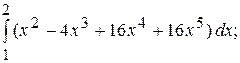 D)
D) 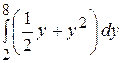 .
.
Правильный ответ: С.
Задание 2. Перечислите основные свойства КРИ-II. Чему равен криволинейный интеграл
![]() , где L –
ломаная линия АВС, А (3, 4), В (1, 2), С (2, 1)?
, где L –
ломаная линия АВС, А (3, 4), В (1, 2), С (2, 1)?
Варианты ответов:
А) ![]() ; В)
-3 ; С)
; В)
-3 ; С) ![]() ; D) -6 .
; D) -6 .
Правильный ответ: В.
Задание 3. Запишите формулу, по которой вычисляется КРИ-II в
случае параметрического задания кривой. Вычислите криволинейный интеграл ![]() , где L –
нижняя половина окружности
, где L –
нижняя половина окружности ![]() ,
проходимая по часовой стрелке.
,
проходимая по часовой стрелке.
Варианты ответов:
А) ![]() ; В)
6 ; С)
; В)
6 ; С) ![]() ; D)
; D) ![]() .
.
Правильный ответ: А.
Задание 4. Вычислите повторный интеграл 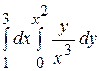 .
.
Варианты ответов:
А) 2; В) 2х; С) ![]() ; D) 3у.
; D) 3у.
Правильный ответ: А.
Задание 5. Дайте определение двойного интеграла, перечислите
его основные свойства. К какому повторному интегралу сводится двойной интеграл
![]() , где D –
область, ограниченная линиями
, где D –
область, ограниченная линиями ![]() ,
, ![]() ?
?
Варианты ответов:
А) 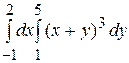 ; В)
; В)
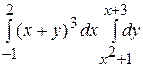 ;
;
С) 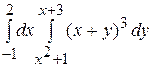 ; D)
; D) 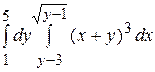 .
.
Правильный ответ: С.
Задание 6. Запишите формулу замены переменных в двойном интеграле. Что такое якобиан? Укажите, чему равен якобиан перехода от декартовых координат (х, у)
1) к полярным координатам ![]() ;
;
2) к обобщенным полярным координатам ![]() , где
, где ![]() ,
, ![]() ;
;
3) к координатам (u, v ),
где ![]() ;
;
4) к координатам (u, v ),
где ![]() .
.
Варианты ответов:
А) -1; В) 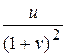 ; С) r ;
D)
; С) r ;
D) ![]() ; Е) 1 ; F) 6r .
; Е) 1 ; F) 6r .
Правильные ответы:
1) С ; 2) F; 3) B; 4) A.
Задание 7. Вычислите с помощью двойного интеграла в полярных координатах площадь
фигуры, ограниченной кривыми ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() .
.
Варианты ответов:
А) ![]() ; В)
; В) ![]() ; С)
2 ; D)
; С)
2 ; D) ![]() .
.
Правильный ответ: D.
Задание 8. Вычислите интегралы:
1) 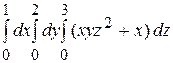 ; 2)
; 2) 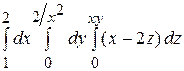 .
.
Варианты ответов:
А) 3; В) ![]() ; С) 16 ;
D) 12; Е)
; С) 16 ;
D) 12; Е) ![]() ; F)
; F) ![]() .
.
Правильные ответы:
1) D; 2) В.
Задание 9. Дайте определение тройного интеграла, перечислите его основные свойства. Как вычисляется тройной интеграл? Расставьте пределы интегрирования в интеграле
![]() , где область V
ограничена плоскостями
, где область V
ограничена плоскостями ![]() ,
, ![]() функция
функция ![]() непрерывна в области V.
непрерывна в области V.
Варианты ответов:
А) 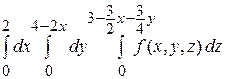 ; В)
; В) 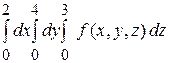 ;
;
С) 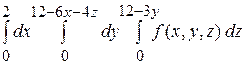 ; D)
; D) 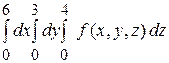 .
.
Правильный ответ: А .
Задание 10. Вычислите с помощью тройного интеграла объем тела, ограниченного
поверхностями ![]() .
.
Варианты ответов:
А) 12; В) 16; С) 6; D) 24.
Правильный ответ: В.
Задание 11. Что называется направляющими косинусами вектора?
1) Найдите единичный вектор нормали ![]() к поверхности
к поверхности ![]() в произвольной точке М
(х, у);
в произвольной точке М
(х, у);
2) Выпишите направляющий косинус ![]() этого вектора
этого вектора ![]() .
.
Варианты ответов:
А) ![]() ;
В)
;
В) ![]() ;
;
С) 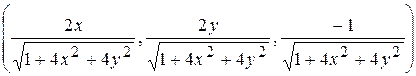 ;
;
D) -1; Е) 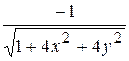 ; F)
; F) ![]() ; G)
; G) 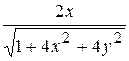 .
.
Правильные ответы:
1) С; 2) Е.
Задание 12. Найдите вектор нормали к плоскости ![]() , который образует
, который образует
1) острый угол с осью OZ;
2) тупой угол с осью OZ;
3) острый угол с осью ОУ;
4) тупой угол с осью ОХ.
Варианты ответов:
А) (3, -2, -1); В) (-3, 2, 1); С) (1, 2, -3); D) (-1, 2, 3).
Правильные ответы:
1) В; 2) А; 3) В; 4) В.
Задание 13. Найдите скалярное произведение ![]() векторного поля
векторного поля ![]() на вектор
на вектор ![]() .
.
Варианты ответов:
А) ![]() ;
;
В) ![]() ;
;
С) ![]() ;
;
D) ![]() .
.
Правильный ответ: В.
Задание 14. Запишите формулу для вычисления потока векторного поля через
ориентированную поверхность (с помощью поверхностного интеграла). К какому двойному
интегралу сводится вычисление потока векторного поля ![]() через плоскость
треугольника
через плоскость
треугольника ![]() , вырезанного из
плоскости
, вырезанного из
плоскости ![]() координатными
плоскостями, в том направлении нормали к плоскости, которая образует с осью ОZ острый угол?
координатными
плоскостями, в том направлении нормали к плоскости, которая образует с осью ОZ острый угол?
Варианты ответов:
А) ![]() , где D – треугольник в плоскости ХОУ с вершинами (0, 0), (4, 0),
(0, -4);
, где D – треугольник в плоскости ХОУ с вершинами (0, 0), (4, 0),
(0, -4);
В) ![]() , где D – квадрат в плоскости ХОУ с вершинами (0, 0), (4, 0), (4,
-4), (0, -4);
, где D – квадрат в плоскости ХОУ с вершинами (0, 0), (4, 0), (4,
-4), (0, -4);
С) ![]() , где D – треугольник в плоскости ХОZ с
вершинами (0, 0), (4, 0), (0, -2);
, где D – треугольник в плоскости ХОZ с
вершинами (0, 0), (4, 0), (0, -2);
D) ![]() , где
D – треугольник в плоскости ХОУ с вершинами (0,
0), (4, 0), (0, -4).
, где
D – треугольник в плоскости ХОУ с вершинами (0,
0), (4, 0), (0, -4).
Правильный ответ: D.
Задание 15. Что называется дивергенцией векторного поля? По какой формуле она
вычисляется в декартовой системе координат? Найдите дивергенцию ![]() векторного поля
векторного поля ![]() в точке М (1, 1,
1).
в точке М (1, 1,
1).
Варианты ответов:
А) -4; В) 4; С) (2, 0, 2); D) (1, -2, 1).
Правильный ответ: В.
Задание 16. Какое векторное поле называется соленоидальным?
Проверьте, является
ли поле ![]() соленоидальным.
соленоидальным.
Варианты ответов:
А) Да; В) Нет; С) ![]() не является векторным
полем;
не является векторным
полем;
D) Для ![]() понятие
соленоидальности не определено.
понятие
соленоидальности не определено.
Правильный ответ: А.
Задание 17. Найдите ротор ![]() векторного
поля
векторного
поля ![]() .
.
Варианты ответов:
А) ![]() ; В)
; В)
![]() ;
;
С) ![]() ; D)
; D) ![]() .
.
Правильный ответ: С.
Задание 18. Какое векторное поле называется потенциальным?
Определите, для
какого векторного поля ![]() функция
функция
![]() является его
потенциалом.
является его
потенциалом.
Варианты ответов:
А) ![]() ;
;
В) ![]() ;
;
С) ![]() ;
;
D) ![]() .
.
Правильный ответ: В.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.