Нахождение компонент связанности графа (Пояснительная записка к курсовой работе), страница 4

Перебор множества вершин

graph:for-each-vertex (graph p)

Функция вызывает заданный предикат p для каждой вершины в графе.

Операции над объектом «множество вершин»

В программе реализованы только необходимые операции над множеством вершин. Набор функций продиктован теми же мотивами, что и набор функций для графа — независимость использующих функций от внутренней организации множества.

Объекты типа «множество вершин» представляются в виде пары («Идентификатор типа», хеш-таблица). Идентификатор типа определяется значением переменной *vertex-set-id*. Значение идентификатора проверяется предикатом проверки типа. Второй элемент пары хранит ссылку на хеш-таблицу, являющуюся множеством вершин графа. Таблица индексирована по именам вершин, а в качестве значений всегда используется nil.

Создание множества вершин графа

vertex-set:build (graph)

Функция создает новое множество, инициализируя его множеством вершин графа graph.

Проверка типа

vertex-set? (set)

Предикат проверяет тип объекта, и возвращает не nil в случае успеха.

Доступ к хеш-таблице

vertex-set:vertexes (set)

Функция предполагается служебной. Возвращает  хеш-таблицу вершин множества. Наличие данной функции позволяет легко ввести дополнительные поля в структуру, описывающие множество, и, таким образом, служит для дальнейшего развития программы.

Поиск любого элемента, входящего во множество вершин

vertex-set:find-vertex (set)

Функция возвращает любой элемент множества set или nil, если set —пустое множество.

Удаление элемента из множества вершин

vertex-set:remove (set x)

Функция удаляет элемент x из множества set и возвращает не nil, если элемент существовал во множестве.

Функция поиска компонент связанности графа

Основной функцией программы является функция find-connected, принимающая один аргумент graph, который являтся графом, для которого требуется найти множество компонент связанности. Функция возвращает список, каждый элемент которого является списком вершин, входящих в одну связанную компоненту графа. Вся работа функции выполняется в локально объявленной функции find, вызывающейся рекурсивно, и возвращающей при каждом вызове одну связанную компоненту графа.

Функция find-connected реализует выбранный алгоритм поиска компонент связанности.

Выбор набора тестов

При выборе тестов для программы, с известной реализацией, необходимо, в первую очередь проверить граничные условия и, при определенной реакции на выход за пределы области определения, граничные запредельные условия. Кроме того, можно провести проверку в пределах области определения.

Граничными условиями, подлежащими проверке, очевидно, являются следующие:

1.  Количество компонент связанности во входном графе.

2.  Количество вершин в каждой компоненте связанности.

Для первого теста выберем пустой граф, не имеющий вершин, и, как следствие, не имеющий компонент связанности. Программа должна вернуть пустой список.

{}

Вторым тестом выберем граф, имеющий только несвязанные вершины (проверка граничных условий по количеству вершин в компоненте связанности). Программа должна вернуть множество компонент связанности, каждый элемент которого содержит только одну вершину.

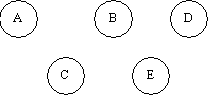
{A},{B},{C},{D},{E}

Третий тест — проверка сильно связанного графа, который, как известно, имеет одну компоненту связанности. Программа должна вернуть множество, состоящее из одного элемента, содержащего все вершины графа.

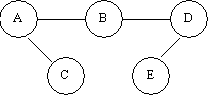
{A,B,C,D,E}

Четвертый, последний, тест (не принадлежащий граничным условиям): граф, имеющий несколько компонент связанности, каждая из которых содержит несколько вершин. Программа должна вернуть соответствующее множество.

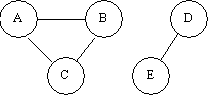
{A,B,C},{D,E}

Заключение